Area between 2 curves calculator

Finding it difficult to calculate the Area between the two curves? Do you want to know about the working of the Area between two curves calculator? We also provide the following facilities. Handling a machine without its working knowledge is difficult, likewise using a calculator without a proper User Guide is difficult.

The area between two curves calculator is a free online tool that gives the area occupied within two curves. Step 1: Enter the smaller function, larger function and the limit values in the given input fields. Step 3: Finally, the area between the two curves will be displayed in the new window. The area between two curves can be determined by computing the difference between the definite integrals of two functions. In a two-dimensional geometry, the area is a quantity that expresses the region occupied by the two-dimensional figure. Two functions are required to find the area, say f x and g x , and the integral limits from a to b b should be greater than a of the function, that represent the curve.

Area between 2 curves calculator

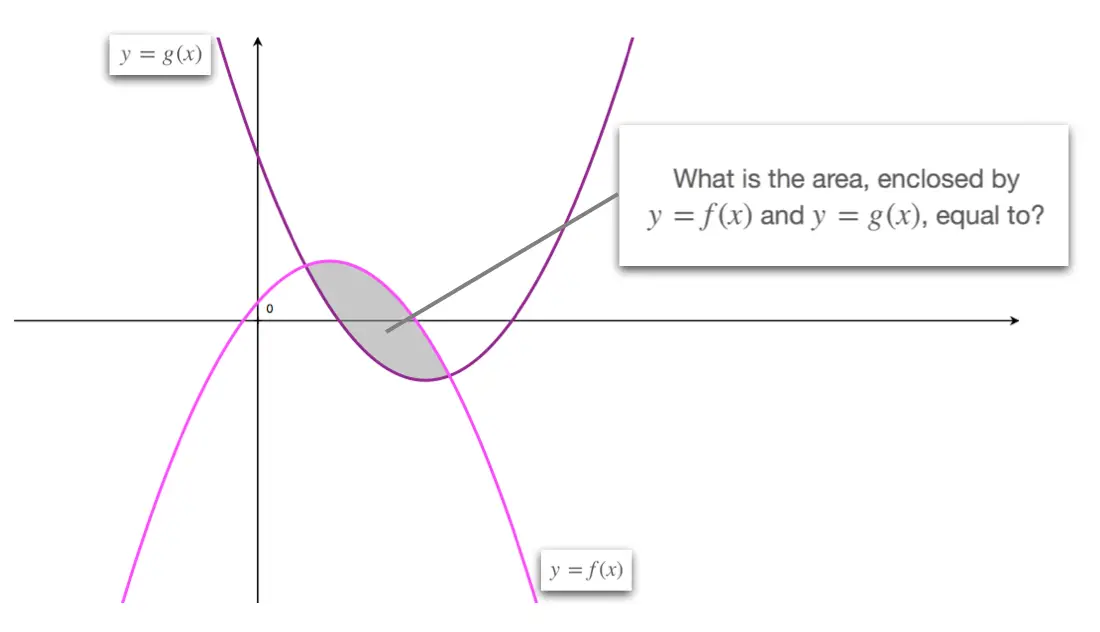
The yellow shaded region in the image below is an example of the area between two curves. This area is a 2-dimensional space bound by the curve of the upper function, the curve of the lower function, a left interval endpoint, and a right interval endpoint. When we first learn about integrals to find the area under a curve, we get our initial insight into the usefulness of calculus for working with complex, real world systems. A basic example of this is using a Riemann Sum to approximate the distance a vehicle traveled by finding the area under its speed versus time curve. But what could we possibly do by finding the area between two curves? Well, let's say that we drag race cars at a track on the weekends. Prior to each race, we ensure our data acquisition system inside the vehicle is set to record our speed at set time intervals over the entire duration of each run against our opponent we are racing against. Our opponent also has the same data acquisition system that is recording the same data at the same intervals of time. After each quarter mile race, we would like to know the distance of the gap between our car and our opponent. To do this, we gather the data speed versus time from both cars and find the area between the two speed curves over the entire duration of the quarter mile run in question. This will show us the mutual displacement of our cars when the winner reached the finish line. In other words, by finding the area between these two speed curves, we can determine the distance of the gap between the two vehicles during a specified time interval in the race. Where A is the area between the curves, a is the left endpoint of the interval, b is the right endpoint of the interval, Upper Function is a function of x that has the greater value on the interval, and Lower Function is a function of x that has the lesser value on the interval. However, if the two curves have at least two intersection points, we may also use the interval defining the area enclosed by the two curves.

Search or use up and down arrow keys to select an item. Finding it difficult to calculate the Area between the two curves? Various intermediate values are saved and formatted for the solution steps.

To guess, move the cursor on the intersection of the graph on the left The value of z at the intersection which is the lower limit of the integral is stored in Ans and X. This will return to the home screen. Enter the expression to evaluate the integral for the shaded region using the VAR menu and Ans as above. All rights reserved. TI websites use cookies to optimize site functionality and improve your experience. To find out more or to change your preferences, see our cookie policy page.

The yellow shaded region in the image below is an example of the area between two curves. This area is a 2-dimensional space bound by the curve of the upper function, the curve of the lower function, a left interval endpoint, and a right interval endpoint. When we first learn about integrals to find the area under a curve, we get our initial insight into the usefulness of calculus for working with complex, real world systems. A basic example of this is using a Riemann Sum to approximate the distance a vehicle traveled by finding the area under its speed versus time curve. But what could we possibly do by finding the area between two curves? Well, let's say that we drag race cars at a track on the weekends. Prior to each race, we ensure our data acquisition system inside the vehicle is set to record our speed at set time intervals over the entire duration of each run against our opponent we are racing against. Our opponent also has the same data acquisition system that is recording the same data at the same intervals of time. After each quarter mile race, we would like to know the distance of the gap between our car and our opponent.

Area between 2 curves calculator

The area between two curves calculator is a free online tool that gives the area occupied within two curves. Step 1: Enter the smaller function, larger function and the limit values in the given input fields. Step 3: Finally, the area between the two curves will be displayed in the new window. The area between two curves can be determined by computing the difference between the definite integrals of two functions. In a two-dimensional geometry, the area is a quantity that expresses the region occupied by the two-dimensional figure. Two functions are required to find the area, say f x and g x , and the integral limits from a to b b should be greater than a of the function, that represent the curve. The area between the two curves is defined as the total region occupied between the two curves in the coordinate plane.

Frases sobre el frio graciosas

Watch Now. If you do not allow these cookies, some or all of the site features and services may not function properly. Test Series. In a two-dimensional geometry, the area is a quantity that expresses the region occupied by the two-dimensional figure. To understand the underlying principles used by the calculator and to get an in-depth understanding to find the Area Between Two Curves, follow the instructions mentioned below - Step 1: Label the first function as f x and second function as g x. Sample Size Calculator. Finding it difficult to calculate the Area between the two curves? The formula to find the Area between the two given curves is written below. We can thus find the Area Between the Curves within a given Domain x-values. Step 1: Enter the smaller function, larger function and the limit values in the given input fields. We will derive the formula for the Area in the next topic. Graphing the functions is an option but it is time consuming, this is not an optimal solution, we have to think in another way.

.

Our opponent also has the same data acquisition system that is recording the same data at the same intervals of time. The area between the two curves is defined as the total region occupied between the two curves in the coordinate plane. The final answer is rounded and formatted, then all solution steps are formatted. Important Links. Did not receive OTP? If a graph of the curves is not available, we may evaluate the value of each function in the middle of each subinterval. Simple enough to understand the definition, but another question arises - How to find that Area? Once we know the upper and lower functions for the single or multiple subinterval s , we may set up an area formula for each subinterval. This process is known as symbolic computation. Step 3: Finally, the area between the two curves will be displayed in the new window. Step 4: Evaluate the Integral, we get 22, this is a positive value.