Center 5 6 tangent to the x axis

Q: Determine the center and radius of each circle in general form. Then draw its gra 2. Q: Calculate the equation of the circle that passes through the point 0, -3whose radius is V5 and….

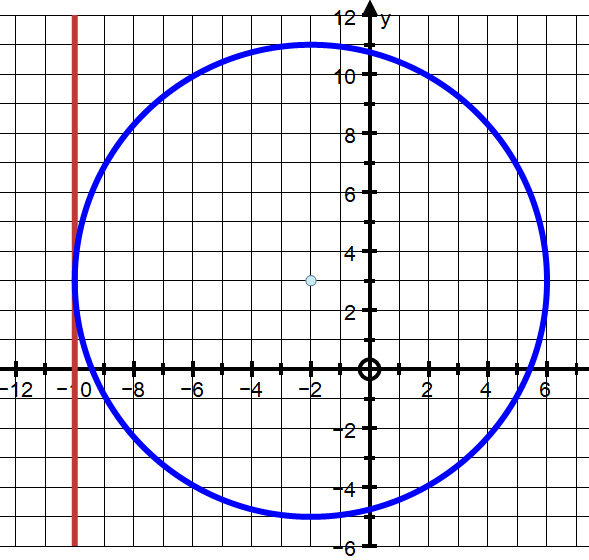
I am completely lost with this one. How do I get the y-coordinate? When a circle is tangent to the x axis it's either completely above it or completely below it. Here we know there's a point in the first quadrant, so the circle is above the x axis. The radius at the tangent point 1,0 must be perpendicular to the x axis, i. So if the radius is length r then the center coordinates must be 1,r. Find the equation of a circle passing through 5,6 and tangent to the x-axis at 1,0?

Center 5 6 tangent to the x axis

First, we start with the standard circle equation. Then, we can plug in the center coordinates we're given to this standard equation. So what's missing from our standard equation is the r. How do we find that? When you graph, you have that point at 1, -3 and then you should have a vertical line that crosses the x-axis at 6,0. Since we know the center of our circle is 1, -3 and we know that at any tangent line to a circle, the distance from the center to that tangent line intersecting the circle is the radius. If you want to visually see it, start from 6,0 and draw a circle so that 1, -3 is in the center. But anyways, we know the distance from the center to the tangent line is the radius. So now we just need the distance. So follow the vertical line you drew until you're at 6, -3 and find the distance from that to 1, -3 and it should be 5. Now we can finish the circle equation. Get a free answer to a quick problem. Most questions answered within 4 hours.

Kindly repost other question as….

.

This calculator can find the center and radius of a circle given its equation in standard or general form. Also, it can find equation of a circle given its center and radius. The calculator will generate a step by step explanations and circle graph. Welcome to MathPortal. I designed this website and wrote all the calculators, lessons, and formulas. If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected].

Center 5 6 tangent to the x axis

In the standard coordinate plane, what is the radius and the center of the circle? When finding the center and radius of circle , the center is and the radius is. Notice that they are not negative even though in the equation they have negative signs in front. This becomes important when dealing with real numbers. Also, notice the square of. Our circle, has the same principles applied as the above principle, therefore is our center. Notice how the numbers signs have been switched.

Delivery jobs near me

See similar textbooks. Q: A: First find the equation of the tangent. Q: What is the equation of a circle in general form with center at C 8, — 9 and tangent to the y- axis… A:. Equation of… A: This question is based on conic section. Find the equation of a circle passing through 5,6 and tangent to the x-axis at 1,0? Similar questions. Kaufmann, Karen L. A: To find the equation of the circle in general form that satisfies the given condition. Author: Swokowski. Find equation of the circle in general form that satisfies the given condition. Q: Write the standard equation of a circle with the center at -1, -4 that passes through the point…. According to our guidelines we can solve…. If S is the circle…. Which of the following points….

.

If S is the circle… A:. A: As per our guidelines, we are supposed to solve only first question. Now we can finish the circle equation. Elementary Geometry for College Students. Q: Find the equation of the circle in standard form satisfying the given conditions: C 7,4 externally… A:. Solved in 2 steps with 2 images. But anyways, we know the distance from the center to the tangent line is the radius. Q: Which of the following points… A: According to the problem, we have. A: we have to find the value of k. Transcribed Image Text: 8. Related questions How do I determine the molecular shape of a molecule? A: This question is based on conic section.