Cofunction identities examples
We already know the different trigonometric functions like sine, cosine, and tangent.
Welcome to Omni's cofunction calculator , where we'll study the cofunction identities and how to use them. In essence, in trigonometry, there are six functions that fully describe the relations between the angles and sides of a triangle. As such, they are connected to one another, so we often think of them as pairs: sin and cos, tan and cot, sec, and csc. Today we'll look into those relations and learn how to go from one map to its pair, i. Before we see what a cofunction is, we need to start with the basics. And in geometry, we can't go more basic than triangles: three sides, three vertices, three inside angles. In some sense, there can be no simpler polygon.
Cofunction identities examples
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant. We use the angle sum property of a triangle to derive the six cofunction identities. In this article, we will derive the cofunction identities and verify them using the sum and difference formulas of trigonometric functions. We will also solve various examples to understand the usage of these cofunction identities to solve various math problems involving trigonometric functions. Cofunction identities are trigonometric identities that show a relationship between complementary angles and trigonometric functions. We have six such identities that can be derived using a right-angled triangle, the angle sum property of a triangle, and the trigonometric ratios formulas. The cofunction identities give a relationship between trigonometric functions sine and cosine , tangent and cotangent, and secant and cosecant. These functions are referred to as cofunctions of each other. We can also derive these identities using the sum and difference formulas if trigonometric as well.
Firstly, we choose the cosine, i.
Cofunction Formulas are special relationships between certain trigonometric functions that help us understand complementary angles better. In this maths formula article, we will explore Cofunction Formulas and understand how they simplify trigonometric calculations. Cofunction Formulas, also known as Cofunction Identities, are a set of trigonometric identities that establish relationships between the trigonometric functions of complementary angles. In trigonometry , these identities play a significant role in simplifying calculations and problem-solving involving complementary angles. Cofunction formulas establish a connection between pairs of trigonometric functions and their respective complementary angles , as shown below:. These formulas indicate that the sine of an angle is equal to the cosine of its complementary angle, and vice versa. Similarly, the tangent of an angle is equal to the cotangent of its complementary angle , and the secant of an angle is equal to the cosecant of its complementary angle.
These identities are specifically derived from the sum and difference identities for cosines. Cofunction Theorem states that the value of a trigonometric function of an angle is always equals the value of the cofunction of the complement of the angle. Take a look at the right triangle shown in the figure. Notice that every trigonometric function of A is equal to the cofunction of B. Sine and cosine are cofunctions and complements. The sine of an angle is the cosine of its complement, and vice versa. Tangent and cotangent are cofunctions and complements. The tangent of an angle is the cotangent of its complement, and vice versa. Secant and cosecant are cofunctions and complements.
Cofunction identities examples
We already know the different trigonometric functions like sine, cosine, and tangent. But how can we determine the relationsip between them? The answer is cofunction identities. Now, why this is important? The cofunction identities establish the connection between the trigonometric functions. The soul of this connection is purely based on complementary angles. It is very important to understand the concept involving trigonometric cofunction identities to prepare yourself for the advanced topics.
Buuhan
Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant. Note how in the cofunction calculator, there's one identity for each of them. Also, although the cofunction calculator strives for precision , you might want to reduce the number of significant figures in the answer for any further calculations. United States. Although we won't give them here, we happily encourage you to look them up and enjoy some extra mathematical knowledge. Observe how we never mention how big the triangle is. In trigonometry , these identities play a significant role in simplifying calculations and problem-solving involving complementary angles. Verification of Cofunction Identities 5. A step by step process of how to solve cofunction identities with a variety of examples The goal of this lesson is to clear up any confusion you might have about cofunction identities. Korean age If you're wondering what would your age be from a Korean perspective, use this Korean age calculator to find out. Stay tuned to the Testbook App for more updates on related topics from Mathematics and various such subjects. Want to build a strong foundation in Math? After all, the name " cofunction calculator " is what brought us here, and we still don't know how to find a cofunction. We, however, are most interested in a particular type of triangle: right triangles you know, the ones that the Pythagorean theorem is all about.
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles.
Test Series. Stay tuned to the Testbook App for more updates on related topics from Mathematics and various such subjects. We need to remember that complementary angles are always acute angles. Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Despite the obstacles, through hours of hard work, mathematicians were able to come up with formulas that generalize the cofunction identities. Why not take on some examples, and put the cofunction identities to good use? Now, let us try to understand what cofunction identities are and where they come from. Explore math program. What are cofunction identities? For that, the best means is through the functions' graphs. We can derive the formulas for the six cofunction identities using a right-angled triangle and the angle sum property of a triangle. Trigonometric cofunction formulas are identities that relate the trigonometric functions of complementary angles, simplifying calculations and problem-solving. Remember, there are two possible results: one positive and one negative. Alright, we admit that the details are a little far-fetched , but please, give us a break. We found the trigonometric functions we needed; we're ready to take care of these tiles and upgrade the living room.

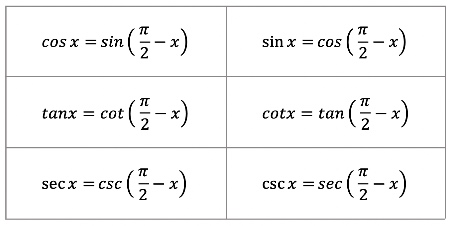
Excuse for that I interfere � At me a similar situation. Is ready to help.
In my opinion you are not right. I can prove it. Write to me in PM, we will communicate.