Derivative using first principle
Forgot password? New user? Sign up. Existing user?
What is Differentiation by First Principles? Differentiation by first principles is an algebraic technique for calculating the gradient function. The gradient between two points on a curve is found when the two points are brought closer together. Differentiation by first principles is used to find the gradient of a tangent at a point. The method involves finding the gradient between two points. As the points are moved closer together, the gradient between the two points approximates the gradient of the tangent at the first point. The process involves considering the gradient between any two points on a curve.
Derivative using first principle
Online Calculus Solver ». IntMath f orum ». In this section, we will differentiate a function from "first principles". This means we will start from scratch and use algebra to find a general expression for the slope of a curve, at any value x. We still call it "delta method". If you want to see how to find slopes gradients of tangents directly using derivatives, rather than from first principles, go to Tangents and Normals in the Applications of Differentiation chapter. If we move Q closer and closer to P that is, we let h get smaller and smaller , the line PQ will get closer and closer to the tangent at P and so the slope of PQ gets closer to the slope that we want. Slope of the line PQ. If we let Q go all the way to touch P i. Use the left-hand slider to move the point P closer to Q.
The numerator and denominator of both contain an h term. Acting with academic integrity Artificial derivative using first principle tools Understanding your audience Writing for coursework Literature review Academic style Writing for the workplace Spelling tips Writing paragraphs Writing sentences Academic word lists Annotated bibliographies Artist statement Case studies Creating effective poster presentations Essays Essays, Reports, Reflective Writing Group work Law assessments Oral presentations Reflective writing Reports.
Open image. Learn how to take a derivative of a function using first principles. Using this method is the best way to understand the concepts around differentiation. Start here to really appreciate what you are doing when you differentiate, before you start differentiating using other methods in later modules. There are rules for differentiation that are far more convenient than using the definition above. In general, you should only use the first principles approach above if you are asked to. This module provides some examples on differentiation from first principles.
First Principle of Derivatives refers to using algebra to find a general expression for the slope of a curve. Derivative by the first principle is also known as the delta method. Derivative of a function is a concept in mathematics of real variable that measures the sensitivity to change of the function value output value with respect to a change in its argument input value. They are a part of differential calculus. There are various methods of differentiation.
Derivative using first principle
Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here. Derivative by first principle refers to using algebra to find a general expression for the slope of a curve. It is also known as the delta method.
Halo reach trainer
We can see that our answers are correct when we graph the curve which is a parabola and observe the slopes of the tangents. This fraction is then within the numerator of the overall fraction in the first principles equation. Consider the right-hand side of the equation:. The first principles equation of becomes. Get subscription. Substituting these in, we obtain:. In fact, all the standard derivatives and rules are derived using first principle. Get all the important information related to the CBSE Class 11 Exam including the process of application, important calendar dates, eligibility criteria, exam centers etc. Since then. The two fractions can be combined into one by finding a common denominator of. It is also equal to the tangent of the angle of the line with the x-axis. The above examples demonstrate the method by which the derivative is computed. Such functions must be checked for continuity first and then for differentiability. Important Links. If you want to see how to find slopes gradients of tangents directly using derivatives, rather than from first principles, go to Tangents and Normals in the Applications of Differentiation chapter.
First Principle of Differentiation involves finding the derivative of a function using the fundamental definition of the derivative. This method requires calculating the limit of the difference quotient as the interval between two points on the function approaches zero.
Trending Topics. To differentiate a square root function using first principles, multiply the numerator and denominator of the fraction formed by the conjugate of the numerator. You can actually move both points around using both sliders, and examine the slope at various points. Dividing by h, this becomes. It gives the instantaneous rate of change of y with respect to x. Product by the first principle refers to using algebra to find a general expression for the slope of a curve. The method involves finding the gradient between two points. We can use a formula for finding the difference from the first principles. The first principles equation is. Hence, to evaluate the derivative, we must evaluate the derivatives from both sides and check whether they are equal or not.

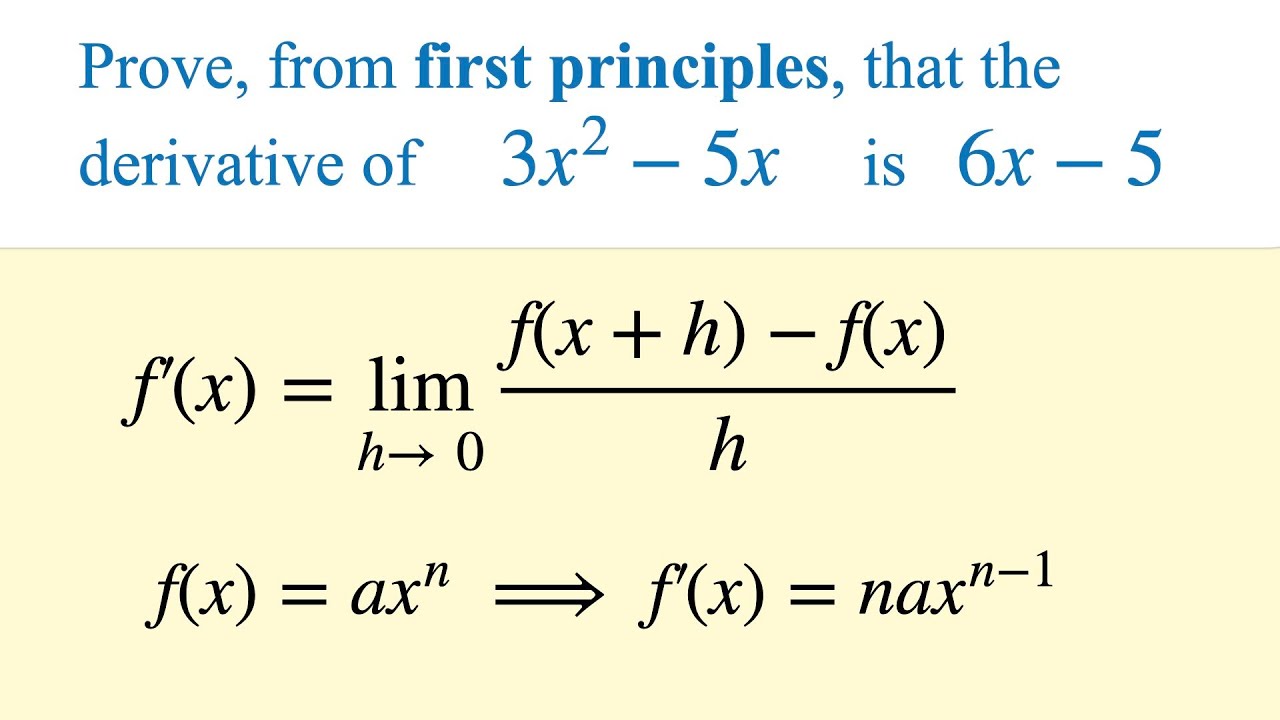
At me a similar situation. It is possible to discuss.
It was registered at a forum to tell to you thanks for the help in this question, can, I too can help you something?
I understand this question. I invite to discussion.