Equal chords are equidistant from the centre

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line.

In the realm of Mathematics, a chord can be described as a line segment that connects two points on a circle's circumference. Interestingly, a circle can have an infinite number of chords. The distance of a line from a point is typically determined by the perpendicular distance from that point to the line. When you draw numerous chords in a circle, you'll notice that the longer chords are closer to the circle's centre than the shorter ones. This article delves into the theorem and proof concerning equal chords and their distance from the centre, as well as its converse theorem. Equal chords in a circle or congruent circles have equal distances from the centre or centres.

Equal chords are equidistant from the centre

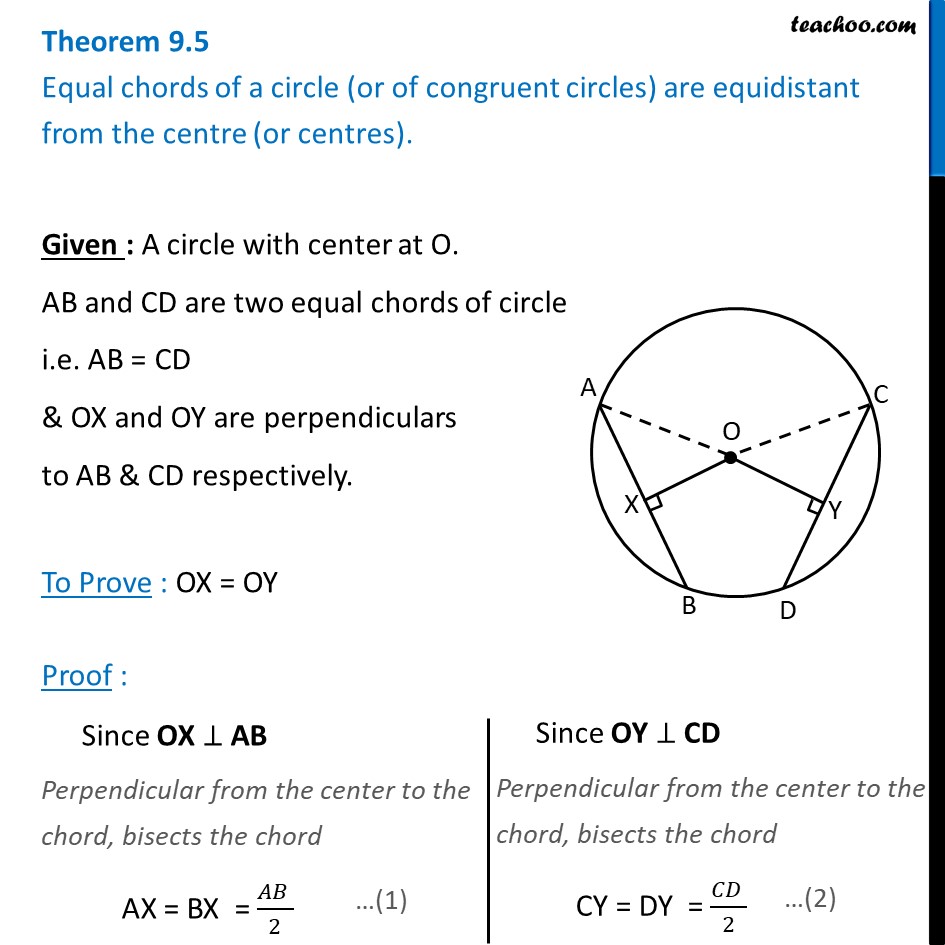
Last updated at March 8, by Teachoo. Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class. Theorem 9. Given : A circle with center at O. AB and CD are two equal chords of circle i. Davneet Singh has done his B. Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. Your browser does not support the audio element. Maths Classes. Old search 1. Old search 2. Old search 3. Trending search 1.

Circular Road of Radius 20 m. Example Problem: Two intersecting chords of a circle form equal angles with the diameter that passes through their intersection point. Add 4 on both sides, we will get.

Well, we see many round objects in daily life like coins, clocks, wheels, bangles, and many more. In this article, we will learn about the equal chords theorem i. And then will learn its converse too. After that, we discussed the theorem regarding the intersection of equal chords. At last, we will learn the diameter is the largest chord of the circle and we will solve examples to understand the concepts more easily. Perpendicular Bisector of the Chord. Here, two points are joined to form a line segment which we call as Chord of the circle.

In the realm of Mathematics, a chord can be described as a line segment that connects two points on a circle's circumference. Interestingly, a circle can have an infinite number of chords. The distance of a line from a point is typically determined by the perpendicular distance from that point to the line. When you draw numerous chords in a circle, you'll notice that the longer chords are closer to the circle's centre than the shorter ones. This article delves into the theorem and proof concerning equal chords and their distance from the centre, as well as its converse theorem. Equal chords in a circle or congruent circles have equal distances from the centre or centres.

Equal chords are equidistant from the centre

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle.

How to remove crank bike

Statement: Chords equidistant from the center of a circle are equal in length. Table Of Two concentric circles. And, for the chord CD:. The distance of the line from a point is defined as the perpendicular distance from a point to a line. And then will learn its converse too. Show More. Remainder Theorem. Hence, proved. Statement: Equal chords of a circle or of congruent circles are equidistant from the center or centers. Demonstrate that the chords are equal. First, join points O and E. Hence it is proven.

If XY is 10, what is the length of AB?

Practice Problems Try solving the following problems. Demonstrate that the chords are equal. We have taken point E which joins from the center. Equal chords of a circle make equal angles at the center of a circle. Hence it is proven. Please login to view more pages. To help Teachoo create more content, and view the ad-free version of Teachooo What is the converse of the theorem related to equal chords and their distances from the centre? Last updated at March 8, by Teachoo. To prove: The chords are equal i. Hence, proved. Did not receive OTP? Circular Road of Radius 20 m. As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as. Perpendicular Bisector of the Chord.