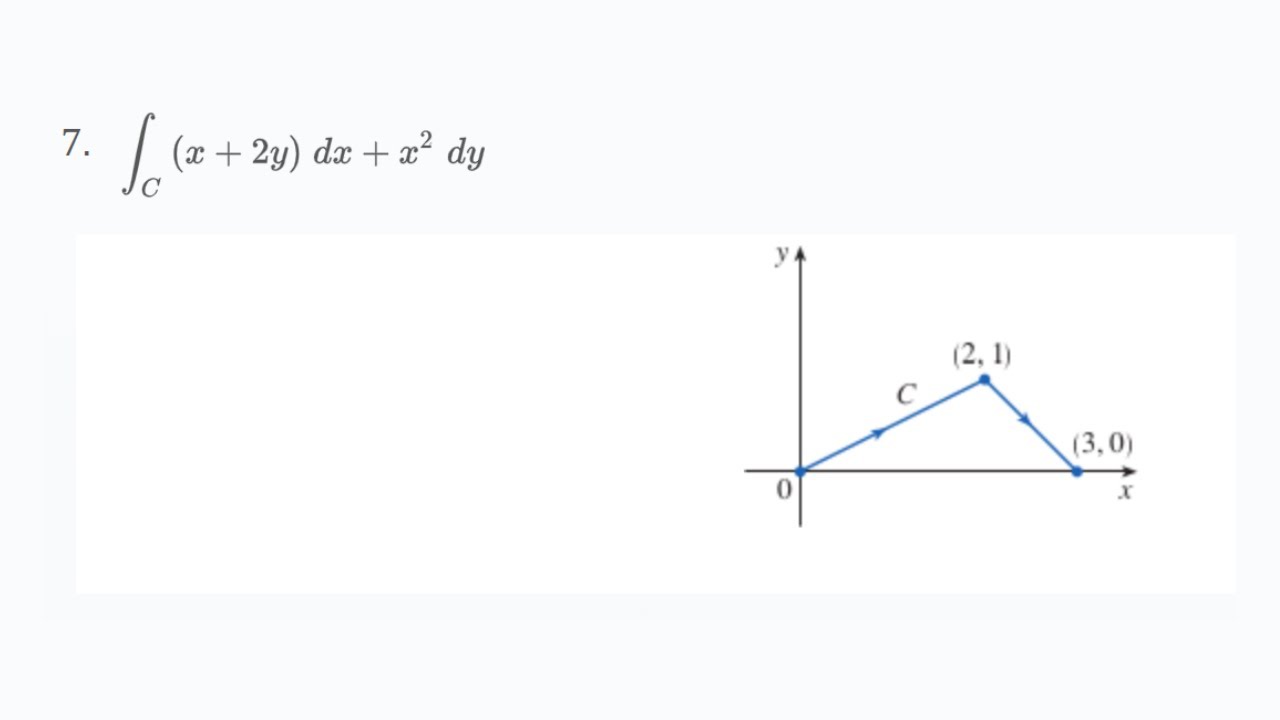
Evaluate the line integral where c is the given curve

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral.

We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''. As with other integrals, a geometric example may be easiest to understand. What is the area of the surface thus formed? We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come. As usual, we start by thinking about how to approximate the area. We pick some points along the part of the parabola we're interested in, and connect adjacent points by straight lines; when the points are close together, the length of each line segment will be close to the length along the parabola.

Evaluate the line integral where c is the given curve

Q: Evaluate the line integral, where C is the given curve. Q: evaluate the line integral along the curve C. Q: Find the line integral of x ds over C where c is the line segment from 1,0 to 0,1 using two…. A: Given. A: Line integral. Q: Evaluate the line integral, where C is the given cu curve. A: C consist line from A 2, 0, 1 to B 3, 3, 1 Now,. A: Find the equation of line in parametric form. C: x-axis from 0, 0 to 0, -3 …. Q: Evaluate the line integral along the given paths. A: We need to evaluate,. For a ,.

Short Answer Expert verified.

Evaluate the line integral, where C is the given curve. Use a calculator or CAS to evaluate the line integral correct to four decimal places. Short Answer Step-by-step Solution. Now share some education! Short Answer Expert verified.

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space. Vector line integrals are integrals of a vector field over a curve in a plane or in space.

Evaluate the line integral where c is the given curve

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space.

Ikea drawer set

Because of Equation 6. Notice that this is the same problem as Example 6. The Chain Rule 5. Q: Evaluate the line integral along the curve C. Linearity of the Derivative 3. McGraw-Hill Education. True or False? Functions 4. Find the work done by a person weighing lb walking exactly one revolution up a circular, spiral staircase of radius 3 ft if the person rises 10 ft. However, there is no reason to restrict ourselves like that. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space.

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course.

We can do line integrals over three-dimensional curves as well. Advanced Engineering Mathematics. Alternating Series 5. To do this, we use Equation 6. FREE Signup. Submit feedback. Square Root Of 3. A line integral is also called the path integral or a curve integral or a curvilinear integral. Chapter Review. We should also not expect this integral to be the same for all paths between these two points. Note that often when dealing with three-dimensional space the parameterization will be given as a vector function. Sketch or graph the solution. A: Using green's theorem.