Factor x 2 4
Solve Practice Play. Game Central.
The student should begin this chapter with a review of the idea of factoring integers. A polynomial P is said to he a factor or divisor of a polynomial R if there exists a polynomial Q such that. Note that Q is also a divisor of R. In this chapter we will agree that our polynomials are to have only integral coefficients. For example,.
Factor x 2 4
Does the sight of a number or expression accompanied by the instructions, "Factor completely," strike fear into your heart? Wish you paid attention in algebra? First off, what is a factor? For example, the number 5 has two factors: 1, and 5. The number 6 has four factors: 1, 2, 3, and 6. The number 5 in this case would have four factors: -5, -1, 1, and 5. Natural numbers are numbers without fractions, starting from 1, 2, 3, 4, Integers are natural numbers, as well as their negative counterparts and 0, or Factoring numbers with the natural number set is simple. Every number has at least two factors. To find other factors, start dividing the number starting from two and working your way up until you reach that number divided by 2. Any quotient that does not have a remainder means that both the divisor and the quotient are factors of that number. Say you need to factor the number 9. You can't divide by two evenly, so we skip it. Note the solution, 4.
New Example. Then square root the 4.
Number and Algebra : Module 33 Years : PDF Version of module. Proficiency with algebra is an essential tool in understanding and being confident with mathematics. For those students who intend to study senior mathematics beyond the general level, factoring is an important skill that is frequently required for solving more difficult problems and in understanding mathematical concepts. In arithmetic, finding the HCF or LCM of two numbers, which was used so often in working with fractions, percentages and ratios, involved knowing the factors of the numbers involved.
In multiplication, factors are the integers that are multiplied together to find other integers. In this example, 6 and 5 are the factors of Essentially, an integer a is a factor of another integer b , so long as b can be divided by a with no remainder. Factors are important when working with fractions, as well as when trying to find patterns within numbers. Prime factorization involves finding the prime numbers that, when multiplied, return the number being addressed. It can be helpful to use a factor tree when computing the prime factorizations of numbers. Using
Factor x 2 4
We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly. Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter.
Hanging prisms
There are expressions that are irreducible over the rational numbers, but which can be factored if we allow irrational numbers. The method of factoring a common term from a given polynomial is based on the distributive laws, which we recall from Chapter 1,. The number 6 has four factors: 1, 2, 3, and 6. Alan P. Quadratic equations such as this one can be solved by a new direct factoring method that does not require guess work. Exercise 3 a By expanding, check each of these identities. Note that the first two signs in the expression are switched. Natural numbers are numbers without fractions, starting from 1, 2, 3, 4, We can then proceed to factor further. Now that you have a trinomial of power two, you can go back and factor it. Factoring a 4 - b 4 We can factor a difference of fourth powers and higher powers by treating each term as the square of another base, using the power to a power rule. One such application is to mental arithmetic.
Wolfram Alpha is a great tool for factoring, expanding or simplifying polynomials.
Then you look at the exponents' powers. Solve Practice Play. One such application is to mental arithmetic. Subtract them, and you'll get x Now we apply this idea to some examples. The simplest type of factoring involves taking out a common factor from two or more terms. It is better for students to be on the look out for the difference of squares identity and apply it directly. However, by adding and subtracting the term , we arrive at a difference of squares. Since there is no other common factor, 2 x is the highest common factor. This expression is ready for the next step. Factoring can give us useful information regarding an expression as the following exercise shows. Log in Forgot Password. How does this help you factor? Multiply the number and variable together to get 2x.

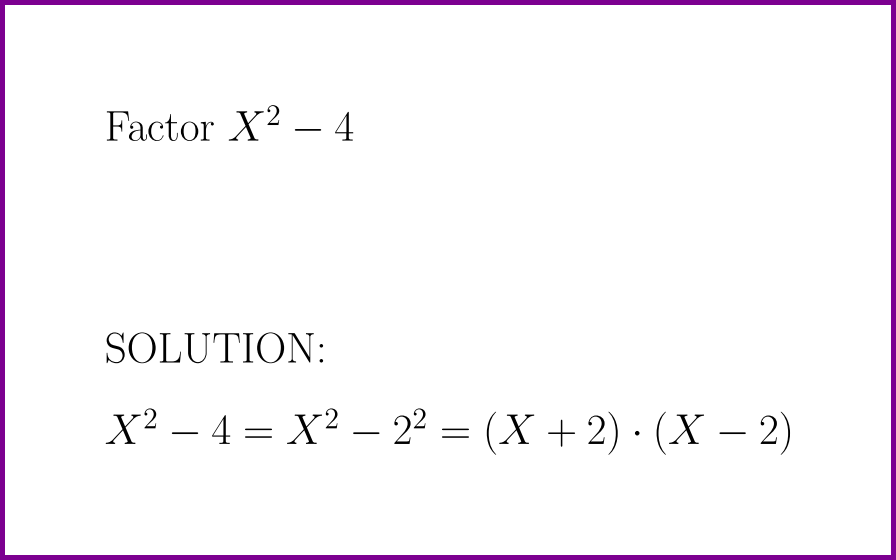
I with you agree. In it something is. Now all became clear, I thank for the help in this question.
You commit an error. I can prove it.