Integral of sinx
Today we have a tough integral: not only is this a special integral the sine integral Si x but it also goes from 0 to infinity!
Integral Calculus is the process of summing up small parts of something into one. In mathematics, it is the process of doing the sum total of functions. There are so many functions in mathematics that can be integrated. Trigonometric functions too can be integrated. In this article, we will study the integral of sin x dx, its formula, derivation with proof, graph along with some solved examples. At the simplest level, integration is the process of combining two or more things to create a whole.
Integral of sinx
Integral of sinx along with its formula and proof with examples. Also learn how to calculate integration of sinx with step by step examples. In calculus , the integral is a fundamental concept that assigns numbers to functions to define displacement, area, volume, and all those functions that contain a combination of tiny elements. It is categorized into two parts, definite integral calculator and indefinite integral. The process of integration calculates the integrals. This process is defined as finding an antiderivative of a function. Integrals can handle almost all functions, such as trigonometric, algebraic, exponential, logarithmic, etc. This article will teach you what is integral to a trigonometric function sine. You will also understand how to compute integration formula sinx by using different integration techniques. The integral of sin x is an antiderivative of the sine function which is equal to —cos x. It is also known as the reverse derivative of sine function w, arigonometric identity. The sine function is the ratio of the opposite side to the hypotenuse of a triangle which is written as:.
Maths Games.
Before going to find the integral of sin x, let us recall what is integral. An integral is also known as the antiderivative. Antiderivative, as its name suggests, is found by using the reverse process of differentiation. Thus, the integration of sin x is found by using differentiation. Let us see more about the integral of sin x along with its formula, proof, and graphical intuition. The integral of sin x is -cos x.
In this section we look at how to integrate a variety of products of trigonometric functions. These integrals are called trigonometric integrals. They are an important part of the integration technique called trigonometric substitution , which is featured in Trigonometric Substitution. This technique allows us to convert algebraic expressions that we may not be able to integrate into expressions involving trigonometric functions, which we may be able to integrate using the techniques described in this section. In addition, these types of integrals appear frequently when we study polar, cylindrical, and spherical coordinate systems later.
Integral of sinx
Before going to find the integral of sin x, let us recall what is integral. An integral is also known as the antiderivative. Antiderivative, as its name suggests, is found by using the reverse process of differentiation. Thus, the integration of sin x is found by using differentiation.
Lovejoy tv
Of course, this doesn't give the exact area. Like Loading The integral of sin x is -cos x. Let us make it what we wanted by multiplying both sides by Let us see some examples. Type your email…. Happy math. Therefore, to obtain the integral of sine, we have to multiply the above equation by a negative sign, that is:. Email Required Name Required Website. Comment Reblog Subscribe Subscribed. Log in now.
Functions involving trigonometric functions are useful as they are good at describing periodic behavior. This section describes several techniques for finding antiderivatives of certain combinations of trigonometric functions.
Continue reading about second order derivatives. What is the integral of sin? Maths Puzzles. Although this might look crazy, the answer is really nice! Already booked a tutor? Is it something I did? Our Journey. So we'd expect something like 0. Download Brochure. The derivative of a function calculates the rate of change, and integration is the process of finding the antiderivative of a function. Antiderivative, as its name suggests, is found by using the reverse process of differentiation.

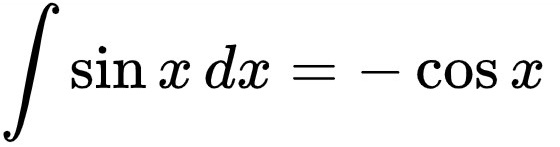
You are mistaken. Write to me in PM, we will communicate.
I confirm. I join told all above. We can communicate on this theme.
I consider, that you are not right. I can defend the position.