Integration of cos root x
The trigonometric substitutions we will focus on in this section are summarized in the table below:. Functions consisting of powers of the sine and cosine can be integrated by using substitution and trigonometric identities.
In mathematics , a nonelementary antiderivative of a given elementary function is an antiderivative or indefinite integral that is, itself, not an elementary function i. Some common non-elementary antiderivative functions are given names, defining so-called special functions , and formulas involving these new functions can express a larger class of non-elementary antiderivatives. The examples above name the corresponding special functions in parentheses. Nonelementary antiderivatives can often be evaluated using Taylor series. Even if a function has no elementary antiderivative, its Taylor series can always be integrated term-by-term like a polynomial , giving the antiderivative function as a Taylor series with the same radius of convergence.
Integration of cos root x
We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. The technique of trigonometric substitution comes in very handy when evaluating these integrals. This technique uses substitution to rewrite these integrals as trigonometric integrals. This integral cannot be evaluated using any of the techniques we have discussed so far. After substituting into the integral, we have. At this point, we can evaluate the integral using the techniques developed for integrating powers and products of trigonometric functions. After we evaluate the integral, we can convert the solution back to an expression involving x. The essential part of this discussion is summarized in the following problem-solving strategy. The following example demonstrates the application of this problem-solving strategy. In this case, the integral becomes. Using this substitution, we have. The procedure for using this substitution is outlined in the following problem-solving strategy. From this equation we obtain:. After multiplying both sides by 2 e y 2 e y and rewriting, this equation becomes:. Use the quadratic equation to solve for e y : e y :.
Commercial Maths. Functions consisting of powers of the sine and cosine can be integrated by using substitution and trigonometric identities. Evaluate the integral using techniques from the section on trigonometric integrals.
Before going to find the integral of cos x, let us recall what is integral. An integral is nothing but the anti-derivative. Anti-derivative, as its name suggests, can be found by using the reverse process of differentiation. Thus, the integration of cos x is found by using differentiation. Let us see more about the integral of cos x along with its formula and proof in different methods.
Integral of cos sqrt x along with its formula and proof with examples. In calculus, the integral calculator follows a fundamental concept that assigns numbers to functions to define displacement, area, volume, and all those functions that contain a combination of tiny elements. It is categorized into two parts, definite integral and indefinite integral. The process of integration calculates the integrals. This process is defined as finding an antiderivative of a function. Integrals can handle almost all functions, such as trigonometric, algebraic, exponential, logarithmic, etc.
Integration of cos root x
In this section we look at how to integrate a variety of products of trigonometric functions. These integrals are called trigonometric integrals. They are an important part of the integration technique called trigonometric substitution , which is featured in Trigonometric Substitution. This technique allows us to convert algebraic expressions that we may not be able to integrate into expressions involving trigonometric functions, which we may be able to integrate using the techniques described in this section. In addition, these types of integrals appear frequently when we study polar, cylindrical, and spherical coordinate systems later. For integrals of this type, the identities. After applying these formulas, simplify and reapply strategies 1 through 3 as appropriate. Use strategy 2. These formulas may be derived from the sum-of-angle formulas for sine and cosine.
Highly paid pornstar
But how to do the integration of cos x? Toggle limited content width. United Kingdom. The Guideline doesn't help us in this scenario. To calculate the approximate areas, we drew the triangles. Use the reference triangle to rewrite the expression in terms of x and simplify. Here, C is the integration constant. If so, we may wish to consider applying an alternative technique. Download as PDF Printable version. Table of contents. Proof of Integral of Cos x by Derivatives 3. Proof of Integral of Cos x by Derivatives. We are going to find the integral of cos x in various methods such as using the derivatives and using the substitution method in the upcoming sections. The trigonometric substitutions we will focus on in this section are summarized in the table below:.
Wolfram Alpha is a great tool for calculating antiderivatives and definite integrals, double and triple integrals, and improper integrals.
The horizontal leg is labeled —a and is on the negative x-axis. In mathematics , a nonelementary antiderivative of a given elementary function is an antiderivative or indefinite integral that is, itself, not an elementary function i. The power of secant is odd and the power of tangent is even: No guideline. ISBN Integral of Cos x Before going to find the integral of cos x, let us recall what is integral. Multiplication Tables. Also, we will calculate the exact areas by using the definite integral of cos x within the same intervals and compare both results. To calculate the approximate areas, we drew the triangles. So we always ignore C while calculating the definite integral. Functions consisting of powers of the sine and cosine can be integrated by using substitution and trigonometric identities. Notice that the integration constant C is NOT present in the definite integral of cos x. Online Tutors. Express the final answers in terms of the variable x. So to find the integral of cos x, we have to see by differentiating what function would give us cos x.

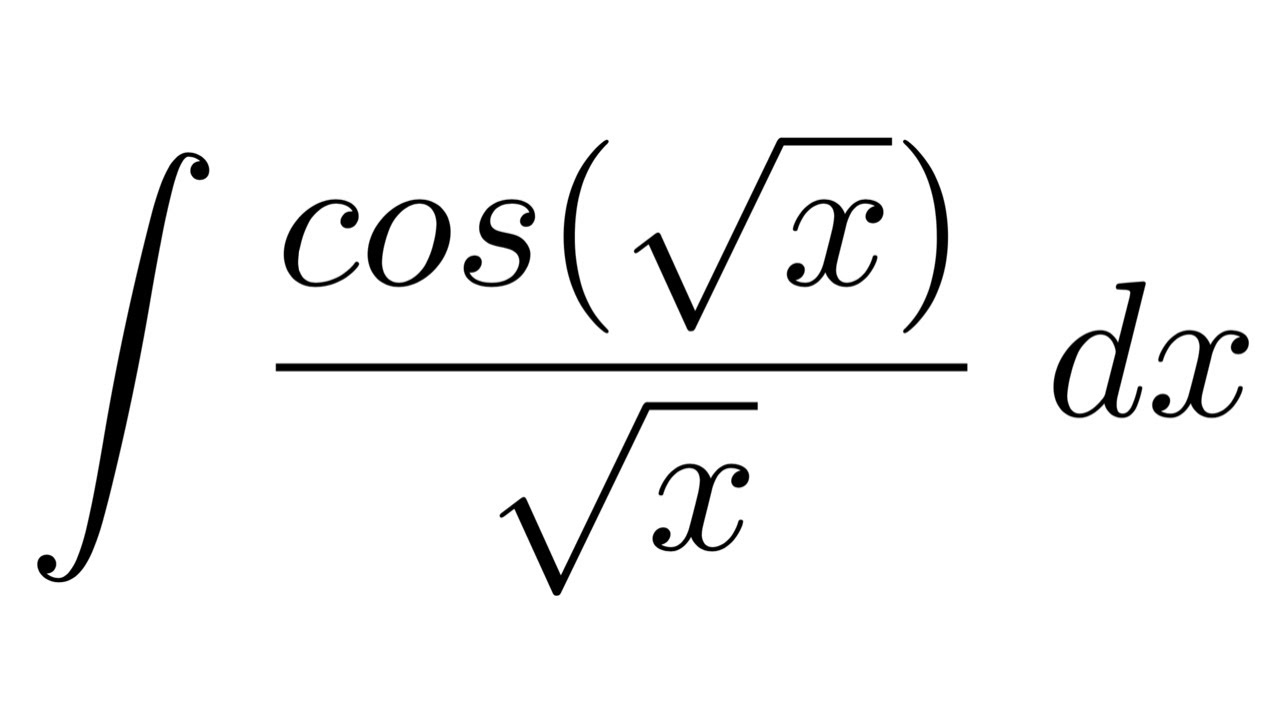
0 thoughts on “Integration of cos root x”