Integration of sin 2x
Magister matematyki Politechniki Poznańskiej.
Wzór Eulera — wzór analizy zespolonej wiążący funkcje trygonometryczne z zespoloną funkcją wykładniczą , określany nazwiskiem Leonharda Eulera. Wzór Eulera został dowiedziony po raz pierwszy przez Rogera Cotesa w w postaci. Zrobił to w , opierając swój dowód na równości szeregów po obu stronach tożsamości. Żaden z nich nie podał interpretacji geometrycznej tego wzoru: utożsamienie liczb zespolonych z płaszczyzną zespoloną powstało około 50 lat później wynik Caspara Wessela. Powyższe wzory służą jako definicje zespolonych funkcji exp, sin i cos, tzn. Przy okazji warto zauważyć, że jest to postać trygonometryczna liczby zespolonej o module jednostkowym. Wzór Eulera stanowi powiązanie analizy i trygonometrii , dostarczając interpretację funkcji sinus i cosinus jako sum ważonych funkcji wykładniczej.
Integration of sin 2x
.
Analogiczne, odejmując od czwarztego równania drugie, mamy. Czy mógłby ktoś pomóc mi z tą całką? Rozwiązanie tej całki z wytłumaczeniem krok po kroku można odnaleźć w lekcji 7 Kursu Całki nieoznaczone:.
.
To find the integral of sin 2 x, we use the cos 2x formula and the substitution method whereas we use just the substitution method to find the integral of sin 2x. Let us identify the difference between the integral of sin 2x and the integral of sin 2 x by finding their values using appropriate methods and also we will solve some problems related to these integrals. For proving this, we use the integration by substitution method. A definite integral is an indefinite integral with some lower and upper bounds. By the fundamental theorem of Calculus , to evaluate a definite integral, we substitute the upper bound and the lower bound in the value of the indefinite integral and then subtract them in the same order. While evaluating a definite integral, we can ignore the integration constant.
Integration of sin 2x
There are of course a very large number 1 of trigonometric identities, but usually we use only a handful of them. The most important three are:. Notice that the last two lines of Equation 1. It is also useful to rewrite these last two lines:. These last two are particularly useful since they allow us to rewrite higher powers of sine and cosine in terms of lower powers. For example:. There are many such tricks for integrating powers of trigonometric functions. Here we concentrate on two families.
Red grouper tavern reviews
BÓŁ pisze:. W innych projektach. Proszę o pomoc z trudną dość całką. Joanna Wojtowicz pisze:. Odejmując od trzeciego równania pierwsze, otrzymamy: , czyli. Artur pisze:. Zostaje więc do policzenia tylko całka z pierwiastkiem. Wynik tego typu całki będzie wyglądał następująco:. Czy ma ktoś może pomysł jak ją rozwiązać? Kategorie : Twierdzenia trygonometrii Liczby zespolone Twierdzenia — analiza zespolona. Wszystkie inne ciasteczka, które nie są niezbędne do funkcjonowania strony, w szczególności zbierające dane osobiste do celów analitycznych, reklamowych i innych. Ten wzór, co jest zaznaczone we wszystkich wzorach na całki, obowiązuje tylko dla nne 1.
Wolfram Alpha is a great tool for calculating antiderivatives and definite integrals, double and triple integrals, and improper integrals.
Zostaje trzecia całka z. Emilia pisze:. Arek pisze:. Inne other. Trygonometria [ edytuj edytuj kod ] Wzór Eulera stanowi powiązanie analizy i trygonometrii , dostarczając interpretację funkcji sinus i cosinus jako sum ważonych funkcji wykładniczej. Dodatkowe , aby obejrzeć zawartość. Dzien dobry, mam problem z rozwiązaniem poniższej całki… Nie mam kompletnie pomysłu jak się za to zabrać, próbowałam przez części jak i przed podstawienie, ale niestety do nieczego mądrego nie doszłam…. Patryk pisze:. Dalej to proste działania na całkach elementarnych. Ewa Gorzeń pisze:. Ja pokonany, a zadanie z fizyki stoi :.

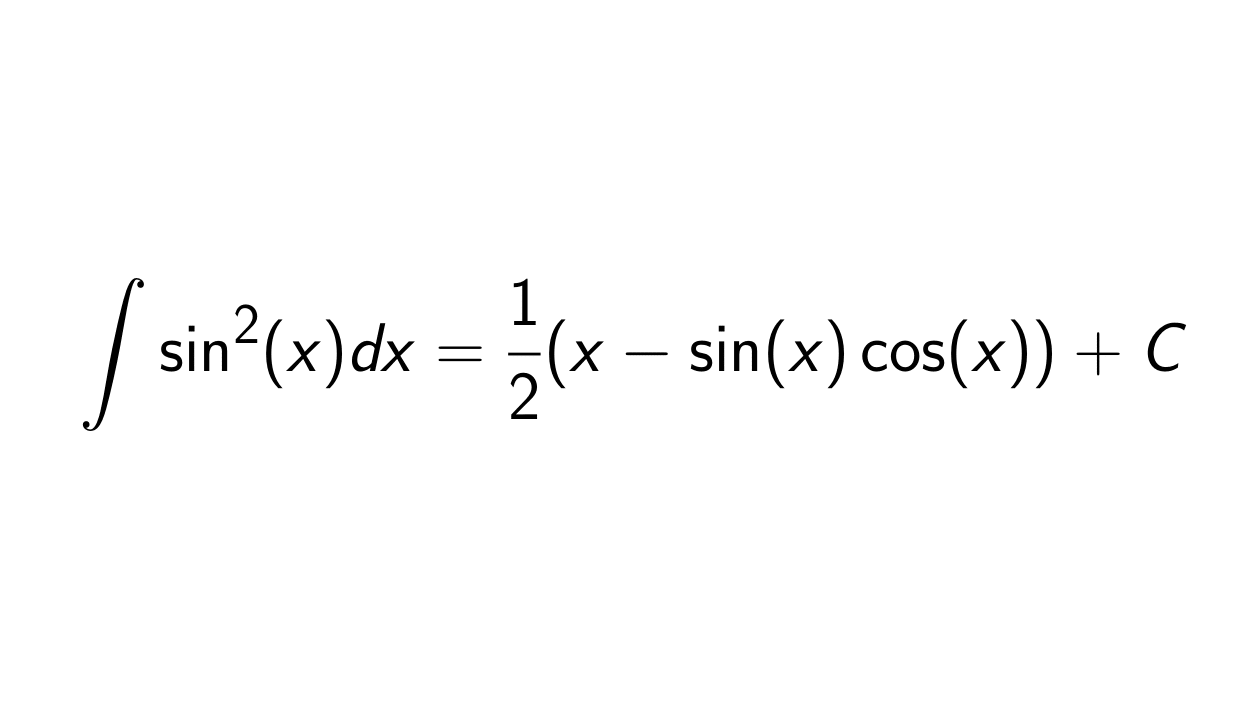
In my opinion you are mistaken. I can prove it. Write to me in PM.
I join told all above.
Should you tell you have deceived.