Length of angle bisector of triangle

The angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangleand ends up on the corresponding opposite side. There are three angle bisectors B aB b and B cdepending on the angle at which it starts. We can find the length of the angle bisector by using this formula:.

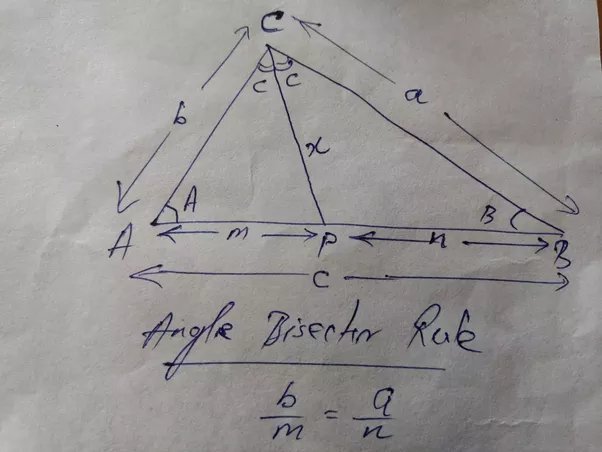
In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle. The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC :. The generalized angle bisector theorem states that if D lies on the line BC , then. When D is external to the segment BC , directed line segments and directed angles must be used in the calculation. The angle bisector theorem is commonly used when the angle bisectors and side lengths are known.

Length of angle bisector of triangle

.

Save my name, email, and website in this browser for the next time I comment.

.

As per the Angle Bisector theorem , the angle bisector of a triangle bisects the opposite side in such a way that the ratio of the two line segments is proportional to the ratio of the other two sides. Thus the relative lengths of the opposite side divided by angle bisector are equated to the lengths of the other two sides of the triangle. Angle bisector theorem is applicable to all types of triangles. Class 10 students can read the concept of angle bisector theorem here along with the proof. Apart from the angle bisector theorem, we will also discuss here the external angle theorem, perpendicular bisector theorem, the converse of angle bisector theorem. An angle bisector is a straight line drawn from the vertex of a triangle to its opposite side in such a way, that it divides the angle into two equal or congruent angles. The table below shows the statements related to internal and external angle bisector theorems as well as their converse. According to the angle bisector theorem, the angle bisector of a triangle divides the opposite side into two parts that are proportional to the other two sides of the triangle. See the figure below. Hence, according to the theorem, if D lies on the side BC, then,.

Length of angle bisector of triangle

The angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangle , and ends up on the corresponding opposite side. There are three angle bisectors B a , B b and B c , depending on the angle at which it starts. We can find the length of the angle bisector by using this formula:. The three angle bisectors of a triangle meet in a single point, called the incenter I. This point is always inside the triangle. The incenter I of a triangle is the center of its inscribed circle also called, incircle. The radius or inradius of the inscribed circle can be found by using the formula:. Download this calculator to get the results of the formulas on this page. Choose the initial data and enter it in the upper left box.

Weighted plates nc

Download this calculator to get the results of the formulas on this page. Original publication: Cambridge University Press, ] ed. Since supplementary angles have equal sines,. Skip to content Geometry 0. Note : in a triangle these two lines would pass through the two sides which form the angle that is divided by the bisector angle. Read Edit View history. It can be used in a calculation or in a proof. This case is depicted in the adjacent diagram. Heath's authoritative translation plus extensive historical research and detailed commentary throughout the text. Categories : Elementary geometry Theorems about triangles. More precisely if the exterior angle bisector in A intersects the extended side BC in E , the exterior angle bisector in B intersects the extended side AC in D and the exterior angle bisector in C intersects the extended side AB in F , then the following equations hold: [1]. Tags: triangle.

In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle.

The angle bisector theorem is commonly used when the angle bisectors and side lengths are known. A procedure for finding the equation of the angle bisector is based on the following:. The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC :. A History of Greek Mathematics by Thomas Heath algebra timeline arithmetic timeline calculus timeline geometry timeline logic timeline mathematics timeline numbers prehistoric counting numeral systems list. Dover , ISBN , p. Read Edit View history. When D is external to the segment BC , directed line segments and directed angles must be used in the calculation. Original publication: Cambridge University Press, ] ed. We can find the length of the angle bisector by using this formula:. In other projects.