Moment of inertia of square lamina

The moment of inertia of a square lamina about the perpendicular axis through its center of mass is 20 kg per meter square then its moment of inertia about an axis touching its side and in the plane of the lamina will be. Step 2: Calculating moment of inertia about an axis touching its side and in the plane of the lamina. The moment of inertia must be specified with respect to a chosen axis of rotation. Hence, the moment of inertia about moment of inertia of square lamina axis touching its side and in the plane of the lamina is 40 kgm 2.

Imagine a spinning ballerina. Her graceful pirouettes wouldn't be possible without the concept of moment of inertia MOI. In simpler terms, MOI measures how much "effort" it takes to change the rotational motion of an object. It's like a measure of an object's resistance to being spun or stopped. Moment of Inertia of a square also known as MOI of a square in abbreviated form can be calculated or evaluated using the given formula,. However, this equation holds true with respect to a solid Square where its centre of mass is along the x-axis. The sum of the second moment of area of the 2 triangles in regard to their common base is twice the second moment of area of one of the triangles.

Moment of inertia of square lamina

.

We are already familiar with the postulate of Perpendicular axis theorem that. MOI is commonly used to compute angular momentum. Imagine a spinning ballerina.

.

A student may well ask: "For how many different shapes of body must I commit to memory the formulas for their moments of inertia? However, if any are to be committed to memory, I would suggest that the list to be memorized should be limited to those few bodies that are likely to be encountered very often particularly if they can be used to determine quickly the moments of inertia of other bodies and for which it is easier to remember the formulas than to derive them. With that in mind I would recommend learning no more than five. A uniform right-angled triangular lamina about one of its shorter sides - i. I shall now derive the first three of these by calculus. The derivations for the spheres will be left until later.

Moment of inertia of square lamina

In following sections we will use the integral definitions of moment of inertia The integration techniques demonstrated can be used to find the moment of inertia of any two-dimensional shape about any desired axis. Moments of inertia depend on both the shape, and the axis. Pay attention to the placement of the axis with respect to the shape, because if the axis is located elsewhere or oriented differently, the results will be different. We will begin with the simplest case: the moment of inertia of a rectangle about a horizontal axis located at its base. This case arises frequently and is especially simple because the boundaries of the shape are all constants. We will try both ways and see that the result is identical. Our integral becomes. This is the formula for the moment of inertia of a rectangle about an axis passing through its base, and is worth remembering. This will allow us to set up a problem as a single integral using strips and skip the inside integral completely as we will see in Subsection

Espn live cricket score cricbuzz

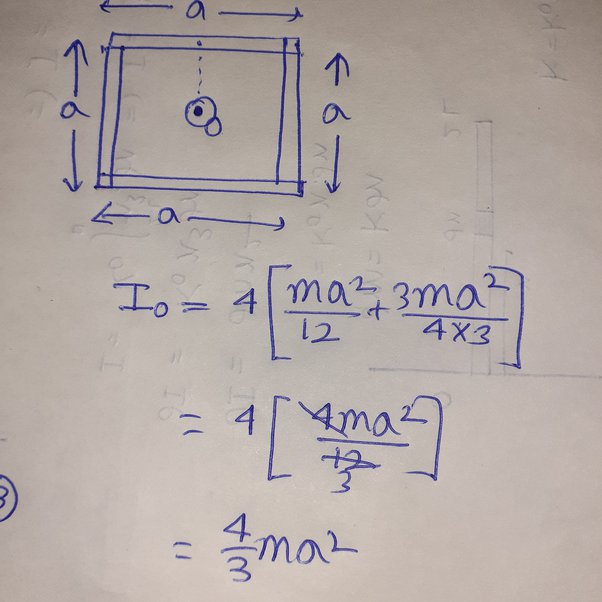
Derivation of Moment of Inertia for a Square. The moment of inertia of the lamina about the tangent A B in the plane of the lamina is The area Moment of Inertia is believed to be a measure of a beam's flexural stiffness in this context. The moment of inertia I of a square can be derived using the parallel axis theorem, which is expressed as:. Moment of Inertia at the poles. Thus, suppose we have a molecule of mass of m located about an axis at d distance. The Moment of Inertia is affected by the following factors:. To minimise power consumption, objects' mass Moment of Inertia must be reduced. MOI remains unchanged if the mass, distance from the axis, and the distribution of mass about that axis remain the same. Moment of Inertia is typically dependent on the distribution of mass about its axis of rotation. When the axis is perpendicular to the plane, it is also designated as J. Find out its Moment of Inertia with respect to an axis touching its side and in the plane of the lamina. In this circumstance, we must consider two scenarios. Applying integration;. We are already familiar with the postulate of Perpendicular axis theorem that,.

We have already discussed a few applications of multiple integrals, such as finding areas, volumes, and the average value of a function over a bounded region. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina flat plate and triple integrals for a three-dimensional object with variable density. The density is usually considered to be a constant number when the lamina or the object is homogeneous; that is, the object has uniform density.

Standard XII Physics. Then, its moment of inertia about an axis touching its side and in the plane of the lamina will be:. MOI about both the axes is the same because of symmetry. The Moment of Inertia is affected by the following factors:. For an axis in a plane, the area Moment of Inertia is generally indicated by the symbol I. Imagine a spinning ballerina. It's like a measure of an object's resistance to being spun or stopped. Further, we will explain the mass per unit area as:. Moment of Inertia at the poles. The mass Moment of Inertia is defined as the resistance to rotation provided by the body owing to its mass. A polar Moment of Inertia is represented by the shaft. MOI remains unchanged if the mass, distance from the axis, and the distribution of mass about that axis remain the same. Moment of Inertia in mass.