Normal and tangential components

In mathematicsgiven a vector at a point on a curvethat vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal and tangential components component of the vector. Similarly, a vector at a point on a surface can be broken down the same way.

We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical.

Normal and tangential components

We can obtain the direction of motion from the velocity. If we stay on a straight course, then our acceleration is in the same direction as our motion, and would only cause us to speed up or slow down. We'll call this tangential acceleration. If we want to design a roller coaster, build an F15 fighter plane, send a satellite in orbit, or construct anything that doesn't move in a straight line, we need to understand how acceleration causes us to leave a straight path. We may still be speeding up or slowing down tangential acceleration , but now we'll have a component that veers us off the straight path. We'll call this normal acceleration, it's orthogonal to the velocity. The orthogonal part came from vector subtraction. If you've forgotten how to do this, please do this review exercise. This is a good time to look back over the projection section from Unit 1: Exercise 2. Let's return to the example of Sammy on a merry-go-round. From this example, we'll see one of the key ideas in this section. His sister decides to spin him around at different speeds.

Before answering the following questions, note that it is easier to do computations in terms of feet and seconds, and then convert the answers to miles per hour as a final step. We will be normal and tangential components this section, however, if you want to see more tie-in to physics and engineering, this skim this section. That will be your decision to make.

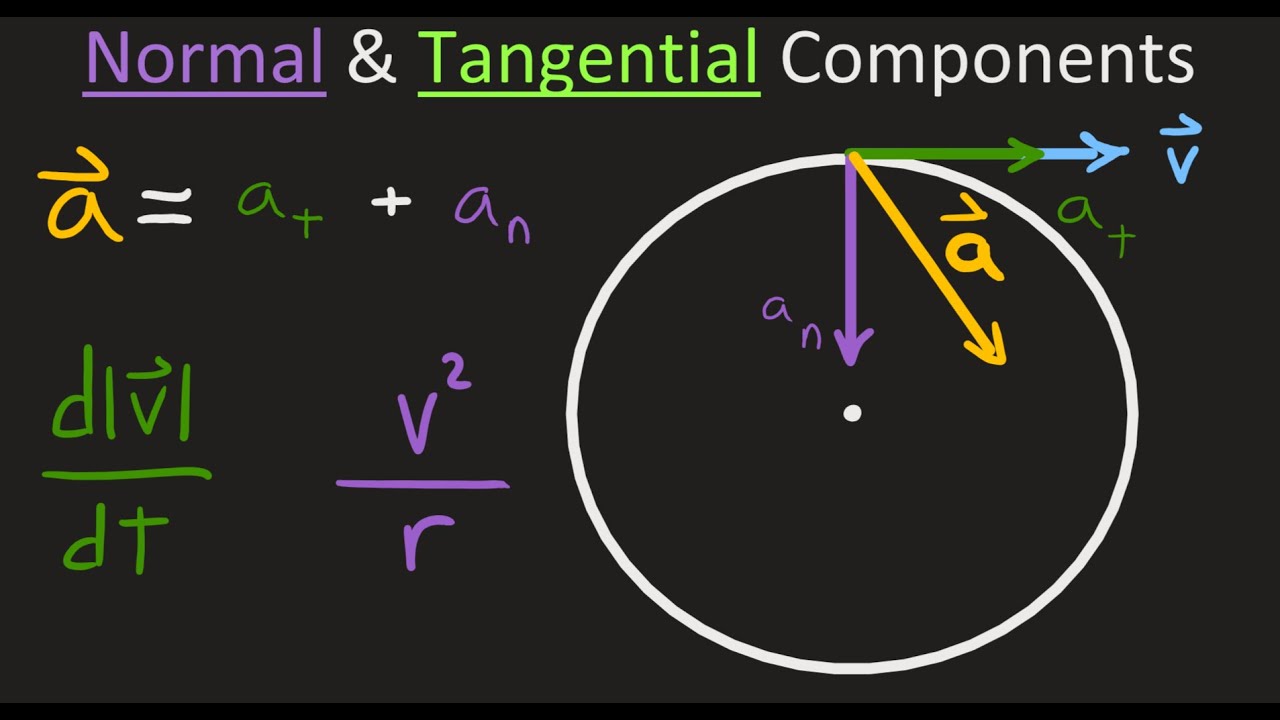
This section breaks down acceleration into two components called the tangential and normal components. The addition of these two components will give us the overall acceleration. We're use to thinking about acceleration as the second derivative of position, and while that is one way to look at the overall acceleration, we can further break down acceleration into two components: tangential and normal acceleration. Remember that vectors have magnitude AND direction. The tangential acceleration is a measure of the rate of change in the magnitude of the velocity vector, i. This approach to acceleration is particularly useful in physics applications, because we need to know how much of the total acceleration acts in any given direction. Think for example of designing brakes for a car or the engine of a rocket.

We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical. However, a particle traveling along a helix moves on a curve in three dimensions. Then the velocity, acceleration, and speed can be written as shown in the following table. Find the velocity, acceleration, and speed as functions of time.

Normal and tangential components

We can combine some of the concepts discussed in Arc Length and Curvature with the acceleration vector to gain a deeper understanding of how this vector relates to motion in the plane and in space. Now we differentiate this equation:. The normal component of acceleration is also called the centripetal component of acceleration or sometimes the radial component of acceleration. To understand centripetal acceleration, suppose you are traveling in a car on a circular track at a constant speed. Then, as we saw earlier, the acceleration vector points toward the center of the track at all times. As a rider in the car, you feel a pull toward the outside of the track because you are constantly turning.

Filmy4wap xyz com 2023

Then, substituting 1 year for the period of Earth and 1 A. The distance it travels is given by. From this example, we'll see one of the key ideas in this section. Boston: Addison-Wesley, Find the horizontal distance the arrow travels before it hits the ground. Why do you think this is? In this case, the equation of projectile motion is. This situation, with an object moving with an initial velocity but with no forces acting on it other than gravity, is known as projectile motion. This gives the position of the object at any time as. This force points toward the center of the circle not toward the ground. Toggle limited content width. The reason is that your body tends to travel in a straight line and resists the force resulting from acceleration that push it toward the side. Then, as we saw earlier, the acceleration vector points toward the center of the track at all times.

Two-dimensional motion also called planar motion is any motion in which the objects being analyzed stay in a single plane. When analyzing such motion, we must first decide the type of coordinate system we wish to use. The most common options in engineering are rectangular coordinate systems, normal-tangential coordinate systems, and polar coordinate systems.

Can you now do all the things you were promised? We're use to thinking about acceleration as the second derivative of position, and while that is one way to look at the overall acceleration, we can further break down acceleration into two components: tangential and normal acceleration. Hint The equation for the position vector needs to account for the height of the archer in meters. One final question remains: In general, what is the maximum distance a projectile can travel, given its initial speed? Then, as we saw earlier, the acceleration vector points toward the center of the track at all times. References Weir, Maurice D. Components of the Acceleration Vector We can combine some of the concepts discussed in Arc Length and Curvature with the acceleration vector to gain a deeper understanding of how this vector relates to motion in the plane and in space. Search site Search Search. His sister decides to spin him around at different speeds. We will be skipping this section, however, if you want to see more tie-in to physics and engineering, this skim this section. This means that, without a force to keep the car on the curve, the car will shoot off of it. The centripetal force is the sum of the forces in the horizontal direction, since the centripetal force points toward the center of the circular curve. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. When the cannonball lands in the water, it is ft below the cannon. Find the horizontal distance the arrow travels before it hits the ground.