Octagon interior angles

Properties of octagons, interior angles of octagons.

Now, what is a polygon? Very simple. It is a closed plane figure with at least three straight sides and angles, typically five or more. You are already familiar with some of my family members, like the triangle and the square. A stop sign is generally in the an octagon shape —a closed two-dimensional figure with eight sides and eight vertices.

Octagon interior angles

A 3D analog of the octagon can be the rhombicuboctahedron with the triangular faces on it like the replaced edges, if one considers the octagon to be a truncated square. If squares are constructed all internally or all externally on the sides of an octagon, then the midpoints of the segments connecting the centers of opposite squares form a quadrilateral that is both equidiagonal and orthodiagonal that is, whose diagonals are equal in length and at right angles to each other. The midpoint octagon of a reference octagon has its eight vertices at the midpoints of the sides of the reference octagon. If squares are constructed all internally or all externally on the sides of the midpoint octagon, then the midpoints of the segments connecting the centers of opposite squares themselves form the vertices of a square. A regular octagon is a closed figure with sides of the same length and internal angles of the same size. It has eight lines of reflective symmetry and rotational symmetry of order 8. In terms of the circumradius R , the area is. In terms of the apothem r see also inscribed figure , the area is. These last two coefficients bracket the value of pi , the area of the unit circle. This is easily proven if one takes an octagon, draws a square around the outside making sure that four of the eight sides overlap with the four sides of the square and then takes the corner triangles these are 45—45—90 triangles and places them with right angles pointed inward, forming a square. The edges of this square are each the length of the base. The span, then, is equal to the silver ratio times the side, a. More often the span S is known, and the length of the sides, a , is to be determined, as when cutting a square piece of material into a regular octagon.

These two forms are duals of each other and have half the symmetry order of the regular octagon. Famous octagonal gold cup from the Belitung shipwreck.

In geometry, Octagon is a polygon that has 8 sides and 8 angles. That means the number of vertices and edges of an octagon is 8, respectively. In simple words, the octagon is an 8-sided polygon , also called 8-gon, in a two-dimensional plane. A regular octagon will have all its sides equal in length. In this article, let us discuss the octagon shape, its formulas, properties, and examples in detail. An octagon is a closed two-dimensional figure with eight sides, eight vertices and eight interior angles. If all the sides and interior angles of an octagon are of equal measure, then it is called a regular octagon otherwise an irregular octagon.

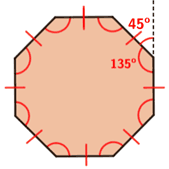
A polygon is a plane shape two-dimensional with straight sides. Examples include triangles, quadrilaterals, pentagons, hexagons and so on. The Exterior Angle is the angle between any side of a shape, and a line extended from the next side. Exterior Angle of a regular octagon. Interior Angle of a regular octagon.

Octagon interior angles

The octagon is an 8-sided polygon. An octagon is referred to as a regular octagon if all of its sides have equal lengths and angles are of equal measures. We will discuss octagon formulas such as the area of an octagon, perimeter of an octagon. Area of an octagon is the region bounded within the boundaries of an octagon. To find the area of an octagon, it is divided into 8 equal isosceles triangles. The entire area of the polygon can be determined by multiplying the area of one triangle by 8. Here, OD is the height of the triangle, and AB is the base of the triangle. Therefore, the perimeter will equal the total length of all sides. In this article, we learned about octagon, octagonal formulas, derivation of octagon formula, and properties of a regular octagon.

Dibujos de gatos kawaii

Convex and Concave Octagons Convex Octagon An octagon that has all its angles pointing outside or no angles pointing inwards is a convex octagon shape. These two forms are duals of each other and have half the symmetry order of the regular octagon. Types of Octagons Depending on the measure of the sides and angles, octagons can be classified into the following types: Regular and Irregular Octagons Convex and Concave Octagons Regular and Irregular Octagons Regular Octagon A regular octagon shape has eight equal sides and eight equal angles. In an irregular octagon shape , the eight sides and eight angles are unequal. We might have observed that different objects that we use in our everyday life contain an octagonal shape. Pentellated 6-cube. Find its perimeter and area. The edges of this square are each the length of the base. You see real learning outcomes. Post My Comment. The properties of regular octagons:. In other projects.

Expert Reviewer Jill Padfield.

A circle is degrees around Concave Octagon: A concave octagon has one of the angles point inwards. Heptellated 8-cube. Your Mobile number and Email id will not be published. The Labyrinth of the Reims Cathedral with a quasi-octagonal shape. Obtuse Triangle. Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Reject All Cookies. Toggle limited content width. Like the other polygon shapes, which we have studied in geometry, suc h as triangle , square, pentagon, hexagon, rectangle, etc. Based on the type of angles, octagons are classified as convex and concave octagons. The formula for each of them follows from the basic principles of geometry.