Quadratic equations practice problems
Solve the equation by factoring:. Solve for :. This is a quadratic equation in standard form, so first we need to factor. By trial and error we find thatso.
If the coefficients of all three terms have a common factor, pull it out. In other words, we need to rearrange the euqation. Multiply the first coefficient by the final term and list off factors. There are two ways to do this. One way involves using the quadratic formula. The quadratic formula is written below.
Quadratic equations practice problems
Here we will learn about the quadratic equation and how to solve quadratic equations using four methods: factorisation , using the quadratic equation formula , completing the square and using a graph. Quadratic algebraic equations are equations that contain terms up to x 2 ; the highest power for a quadratic equation is 2. Quadratic equations are a type of polynomial equation because they consist of two or more algebraic terms. A quadratic equation can have zero , one or two real solutions. At GCSE the solutions to polynomial equations such as quadratics will always give real numbers but they can be either irrational and rational numbers. Includes reasoning and applied questions. In order to solve a quadratic equation we must first check that it is in the form:. Although the most common way of solving quadratic equations is through factorising, there are in fact three other ways to solve them as well. We will explore how to solve the same quadratic equation in each of the four ways. Step-by-step guide: Solving equations.
Correct answer:.
In this article we cover quadratic equations — definitions, formats, solved problems and sample questions for practice. A quadratic equation is a polynomial whose highest power is the square of a variable x 2 , y 2 etc. For every quadratic equation, there can be one or more than one solution. These are called the roots of the quadratic equation. We have to take two numbers adding which we get 5 and multiplying which we get 6. They are 2 and 3. Let us verify that.
The quadratic equation will always have two roots. The nature of roots may be either real or imaginary. A quadratic polynomial, when equated to zero, becomes a quadratic equation. In other terms, a quadratic equation is a second degree algebraic equation. The values of x satisfying the equation are called the roots of the quadratic equation. The values of variables satisfying the given quadratic equation are called their roots. The term b 2 — 4ac in the quadratic formula is known as the discriminant of a quadratic equation. The discriminant of a quadratic equation reveals the nature of roots. Since the discriminant is a perfect square, the difference between two perfect squares in R.
Quadratic equations practice problems
Quadratic equation questions are provided here for Class 10 students. Here, a, b and c are constants, also called coefficients and x is an unknown variable. Also, learn Quadratic Formula here. Solving the problems based on quadratics will help students to understand the concept very well and also to score good marks in this section.
Katie price onlyfans leaked
I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law. This is our answer by the first merthod. Finally, we need two numbers whose product is negative thirty-five and whose sum is positive two. Explanation : This expression involves the difference of two cubic terms. His book, The Elements, is one of the most studied books in human history. This is for simplification purpose. Explanation : This is a quadratic equation in standard form, so first we need to factor. Plug these into the formula. Company name. Possible Answers:. For this kind of equations, we apply the quadratic formula to find the roots. Varsity Tutors. Since must be positive, we throw out the negative solution. We know Billy's and Johnny's current ages; we just need to figure out their future ages.
We can follow the steps given below to solve word problems using quadratic equations.
I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process. Now factor, set each binomial to zero, and solve individually. Example 2: quadratic equation — solve by using the quadratic formula Example of solving a quadratic equation by using the quadratic formula. Substitute and for and and for , then solve for :. Email address: Your name: Feedback:. First: Inside: Outside: Last: Now factor, set each binomial to zero, and solve individually. Still stuck? Till now, the coefficient of x 2 was 1. In order to solve a quadratic equation we must first check that it is in the form:. To factor an expression in this format, we can use a special formula. Let us express the middle term as an addition of 2x and 3x.

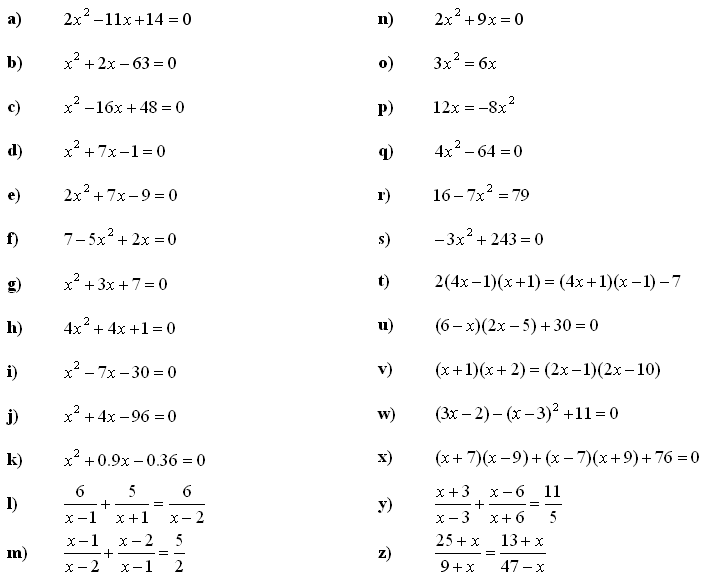
I consider, that you commit an error. Let's discuss it.