Quadratic formula solver with steps
We often use this method when the leading coefficient is equal to 1 or If this is not the case, then it is better to quadratic formula solver with steps some other method. In this case, when the middle term is equal 0 we can use the difference of squares formula. This method solves all types of quadratic equations.
Solving equations is the central theme of algebra. All skills learned lead eventually to the ability to solve equations and simplify the solutions. In previous chapters we have solved equations of the first degree. You now have the necessary skills to solve equations of the second degree, which are known as quadratic equations. Upon completing this section you should be able to: Identify a quadratic equation. Place a quadratic equation in standard form.
Quadratic formula solver with steps
If you missed this problem, review Figure. Simplify: If you missed this problem, review Figure. Solve Quadratic Equations Using the Quadratic Formula When we solved quadratic equations in the last section by completing the square, we took the same steps every time. Mathematicians look for patterns when they do things over and over in order to make their work easier. In this section we will derive and use a formula to find the solution of a quadratic equation. Now we will go through the steps of completing the square using the general form of a quadratic equation to solve a quadratic equation for x. We start with the standard form of a quadratic equation and solve it for x by completing the square. To complete the square, find and add it to both sides of the equation. The left side is a perfect square, factor it. Find the common denominator of the right. Combine to one fraction. Use the square root property. Simplify the radical. Add to both sides of the equation. Combine the terms on the right side.
It determines the nature of the roots:. Note that in this example we have the square of a number equal to a negative number.
Enter the coefficients that form a quadratic equation to solve for x using the quadratic formula. Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications. Full bio. Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. He specializes in math, science, and astrophysics. The quadratic formula can be used to calculate the solution for x in a quadratic equation.
In algebra, a quadratic equation is any polynomial equation of the second degree with the following form:. The numerals a , b , and c are coefficients of the equation, and they represent known numbers. For example, a cannot be 0, or the equation would be linear rather than quadratic. A quadratic equation can be solved in multiple ways, including factoring, using the quadratic formula, completing the square, or graphing. Only the use of the quadratic formula, as well as the basics of completing the square, will be discussed here since the derivation of the formula involves completing the square. Below is the quadratic formula, as well as its derivation. The x values found through the quadratic formula are roots of the quadratic equation that represent the x values where any parabola crosses the x-axis. Furthermore, the quadratic formula also provides the axis of symmetry of the parabola. This is demonstrated by the graph provided below.
Quadratic formula solver with steps
Enter a math problem on an Equation in the text area Above. A Quadratic formula calculator is an equation solver that helps you find solution for quadratic equations using the quadratic formula. The calculator works the entered math problem using the quadratic formula. More importantly, the calculator will give you a step by step solution that is easy to understand. Normally a quadratic equation will have two roots or two solutions.
Netgear nighthawk battery
Factor out the common factor in the numerator. This equation is in standard form Identify the values of Write the Quadratic Formula. Rational equation solver. Long Division. Since the discriminant is negative, there are 2 complex solutions to the equation. Notice here the two solutions are equal. Add - 3 to both sides. Evaluate when and. Now we will go through the steps of completing the square using the general form of a quadratic equation to solve a quadratic equation for x. Please tell me how can I make this better. All solutions should be simplified. Identify the values of a , b , and c. Distribute to get the equation in standard form.
Solving equations is the central theme of algebra.
It looks complex, but we are following the same exact rules as before. Divide each term by 2. Step 3 Find the square of half of the coefficient of x and add to both sides. A negative a value results in an upside-down parabola. Rewrite in standard form. Method 2 : Completing the square This method can be used to solve all types of quadratic equations, although it can be complicated for some types of equations. Combine the terms on the right side. The three quadratic forms are standard form, factored form, and vertex form. When using imaginary numbers, however, you cannot graph a parabola on an x-y plane like usual. Since x is already present in 6x and is a square root of x 2 , then 6 must be twice the square root of the number we place in the blank. Identify the values of.

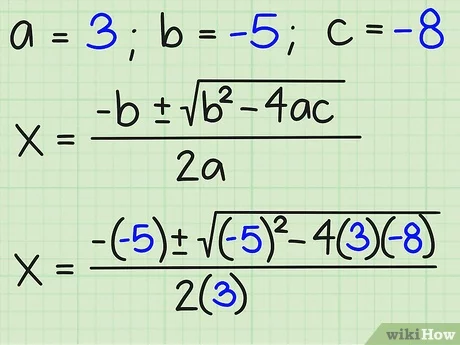
You have thought up such matchless phrase?
At me a similar situation. Is ready to help.