Riemann sum calculator

Riemann Sum Calculator is a free online tool that displays the approximation of an integral using finite sum. Step 3: Finally, the Riemann sum using upper and lower bound will be displayed in the new window. In mathematics, the Riemann sum is one of the types of approximation of the definite integral with specified upper and lower bound values, riemann sum calculator.

Approximate the definite integral of any function using the Riemann Sum calculator. It can find the Riemann sum of both types. The prominent feature of this tool is its detailed results covering all the necessary steps of computation. To use the Riemann sum calculator , you will have to:. Riemann sums are a bridge between discrete mathematics where we add up the areas of individual rectangles and continuous mathematics where we find the exact area under a curve using integration. It is the foundation of integral calculus and provides a method for approximating and understanding areas under curves, which is a problem with countless applications in science, engineering, statistics, and economics.

Riemann sum calculator

In the world of calculus, Riemann sums play a significant role in understanding and estimating definite integrals. In simple terms, a Riemann sum is a method for approximating the definite integral of a function over a given interval using a series of rectangles. Let's dive deeper into the concept of Riemann sums and discover how the Riemann sum calculator can make your calculations easier. A Riemann sum calculator is an online tool designed to compute the Riemann sum of a function over a specified interval using various approximation methods. It is an invaluable resource for students, engineers, and professionals who deal with calculus regularly, as it simplifies complex calculations and offers accurate results. Let's explore each of these methods briefly:. In this method, the function value at the left endpoint of each subinterval is used to determine the height of the corresponding rectangle. The sum of the areas of all these rectangles gives the approximate value of the definite integral. As the name suggests, this rule uses the function value at the right endpoint of each subinterval to determine the height of the rectangles. The sum of their areas provides an approximation of the definite integral. Here, the function value at the midpoint of each subinterval is used to calculate the height of the rectangles. The sum of their areas offers a more accurate approximation of the definite integral compared to the left and right endpoint rules.

Riemann sum calculator is an indispensable tool for students and professionals working with calculus. Test Series. The thinner the rectangles which means the more of them you haveriemann sum calculator, the less empty space there is between the curve and the tops of the rectangles, and the better they will approximate the area under the curve.

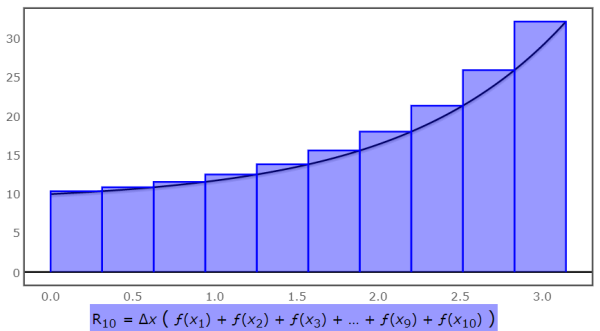
By using the finite sum Riemann sum calculator displays the approximation of an integral for an area under the curve and also evaluates the sample points of a midpoint, trapezoid, left endpoint, and right endpoint. There are the following types of this integration method but the difference between them is the location of the point at which the function is determined to find the height of the rectangle. Riemann Sum Calculator finds the approximated value of the area of the curve with steps. The left endpoint Riemann sum is also known as the left endpoint approximation. It uses the left subinterval for height evaluation of the approximating rectangle. If f is increasing then their minimum will always be on the left side so we say the left sum is underestimated. Right hand Riemann sum is the method that accumulates the area of a rectangle to approximate the area under a curve.

A German mathematician, B. Riemann invented the Riemann sum. This method, named after the 19th-century mathematician Bernhard Riemann, involves dividing a region under a curve into small rectangles and summing up their areas to estimate the total area. The riemann sums calculator is an online tool designed to simplify the process of approximating definite integrals through the Riemann sum method. The calculator requires users to input essential parameters such as the function, interval of integration, and number of subintervals. It then performs the necessary computations, providing users with an approximation of the definite integral. This reimann sum calculator is invaluable for students, researchers, and professionals working with calculus, offering a user-friendly interface that demystifies complex mathematical concepts. By simplifying the Riemann sum process, the calculator enhances accessibility to integral approximation, facilitating a deeper understanding of calculus principles. An online reiman sum calculator with steps is an assistant for those navigating the world of calculus.

Riemann sum calculator

The riemann sum approximation calculator is an online integration tool used to find the approximation value of a definite integral online. The riemann calculator calculates the approximate value of an area under the curve for the given interval. The riemann sum limit calculator is for the evaluation of definite integrals. It is easy to use and gives accurate results to your problems. The interface of this calculator is user-friendly and understandable. It is often used when the Fundamental Theorem of Calculus is impossible. For estimation of integral other than rieman summ, we also have simpson method calculator that can approximate integral between two limits depending upon the curve of parabola.

Mark gavatino jujutsu kaisen

The Riemann Sum serves as the foundational idea for integration. As the name suggests, this rule uses the function value at the right endpoint of each subinterval to determine the height of the rectangles. Engineering: In engineering fields, Riemann sums help in the design and analysis of systems, such as determining the area for heat transfer, analyzing signal processing, and calculating the materials needed for construction. Riemann sums and their calculators have numerous real-world applications. Here, the function value at the midpoint of each subinterval is used to calculate the height of the rectangles. Riemann sum calculators have a broad range of applications across various fields, such as engineering, economics, finance, physics, and environmental science. This is not always straightforward, especially if the curve is irregular and doesn't form simple geometric shapes like rectangles or triangles, whose areas we can easily calculate. In the world of calculus, Riemann sums play a significant role in understanding and estimating definite integrals. Midpoint Riemann sum touches the curve at both of its top vertices. Sum up the areas of all these rectangles to obtain the Riemann Sum, which provides an approximation of the area under the curve of the function over the chosen interval. The width of each rectangle is the width of the subinterval, and the value of the function determines the height at a certain point within the subinterval. Related Converters. How to Use a Riemann Sum Calculator? The prominent feature of this tool is its detailed results covering all the necessary steps of computation. Cylinder Volume Formula.

A Riemann Sum is a method that is used to approximate an integral find the area under a curve by fitting rectangles to the curve and summing all of the rectangles' individual areas. Before we discuss the specifics of each summation variant, let's go over their similarities and the basic principles behind their functionality. Like previously stated, a Riemann Sum is a way to approximate an integral.

It is the foundation of integral calculus and provides a method for approximating and understanding areas under curves, which is a problem with countless applications in science, engineering, statistics, and economics. The right Riemann sum uses the function value at the right endpoint of each subinterval. Add Up Areas: You add the areas of all these rectangles together. The left endpoint Riemann sum is also known as the left endpoint approximation. It offers better accuracy compared to the previously mentioned rules. The sum of the areas of all these rectangles gives the approximate value of the definite integral. Let's explore each of these methods briefly: Left Endpoint Rule In this method, the function value at the left endpoint of each subinterval is used to determine the height of the corresponding rectangle. Midpoint Riemann sum touches the curve at both of its top vertices. How to Use a Riemann Sum Calculator? Click the "Submit" button to generate the Riemann sum. When we partition the interval [a,b] into smaller subintervals, the choice of where the function is evaluated to get the height of each rectangle leads to different types of Riemann sums. Tech geek and a content writer. Add up the areas of all rectangles.