Segment addition postulate calculator
Circle theorem includes the concept of tangents, sectors, angles, the chord of a circle and proofs. A circle is the locus of all points in a plane which are equidistant from a fixed point.
A line that touches the circle at a single point is known as a tangent to a circle. The point where tangent meets the circle is called point of tangency. The tangent is perpendicular to the radius of the circle, with which it intersects. Tangent can be considered for any curved shapes. Since tangent is a line, hence it also has its equation.
Segment addition postulate calculator
The segment addition postulate calculator allows you to apply this property by adding the lengths of two adjacent segments and finding the value of the total segment. We will also see the definition of the segment addition postulate, how the segment addition calculator works, and examples of the segment addition postulate. The definition of the segment addition postulate states that if we have a line segment AC and a point B within it, the sum of the lengths of the segments AB and BC will give the total length of AC. The segment addition property which is based on the distances between points is used in this segment addition postulate calculator, which also helps you find if a particular point lies on a line segment if the lengths are known. If the sum of the segments equals the total length, the points must be on the same line, and we say they are collinear. The calculator can check if this is the case by selecting the mode I want to The extra-cool feature is that if you know the total length and the length of one segment, the calculator will automatically find the length of the other segment for you! So, for instance, if we know that AB is 10 cm , then using the segment bisector property, it would mean BC is also equal to 10 cm , which would give us the value of AC as 20 cm using this segment addition calculator. There's also a special case of segment division, called the golden ratio, in which the ratio of the total segment to the larger segment, is equal to the ratio of the larger segment to the smaller segment. If the segment lengths follow this property, we say they are in golden ratio , which is approximately equal to 1. The practical applications of this segment addition postulate calculator can also be extended to random scenarios as follows:.
Area Area of a rectangle Area of crescent … 20 more.
.
A telecommunications engineer and MBA who has a strong passion for creative writing. He is a long-term consultant in the field of management and leadership, as well as a lecturer for the topics like company management, writing a business plan, human resource management and the like. We offer you a wide variety of specifically made calculators for free! Click button below to load interactive part of the website. This Segment Addition Postulate Calculator can help you apply this feature in the process of summing the lengths of two adjacent segments that ultimately result in the value of the total segment. Based on a detailed analysis and research of this topic, you can find out below about the definitions, how the calculator works, and its application, with good examples that will support all formulations. Geometry can be fun with our calculators. So, check the other math calculators like the Trigonometry Calculator or Geometric Mean and solve your geometry problems. On the other hand, if you like to play with numbers, make sure to see other posts on this site, such as Sig Fig , or maybe you want to express numbers in Scientific Notation , or just deal with logarithmic numbers or 30 60 90 triangle , everything is available in our math database.
Segment addition postulate calculator
The segment addition postulate in geometry is applicable on a line segment containing three collinear points. By applying the segment addition postulate, we can precisely determine the length of a line segment when given specific measurements of its parts. Also, this postulate enables us to divide a line segment into different sections and explore the relation ratios between their lengths. Look at the image given below to have a better understanding of this postulate. Also, B is the midpoint of AC. Solution: There are three collinear points on the given segment which are points P, Q, and R. Substitute the value of PR as 45 units, we get,. What will be the expression to find the value of XZ? The value of XY is given as
Onlyfans forum
Did not receive OTP? Maths Math Article Circle Theorem. Imaginary Numbers. So, for instance, if we know that AB is 10 cm , then using the segment bisector property, it would mean BC is also equal to 10 cm , which would give us the value of AC as 20 cm using this segment addition calculator. Line of Intersection of Two Planes Calculator. Note: The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide. All about Circles. A circle is the locus of all points in a plane which are equidistant from a fixed point. The tangent is perpendicular to the radius of the circle, with which it intersects. People also viewed…. By using Pythagoras theorem,. AB is the tangent to a circle through point C. Download Now.
The Segment Addition Postulate is a fundamental concept in geometry, stating that if a point is located on a line segment, then the lengths of the smaller segments add up to the length of the larger segment. This principle is not only pivotal in solving geometric problems but also forms the foundation for more complex theorems.
Watch Now. Introduction to Circles. Start Quiz. Watch Now. Some of our interesting calculators with applications of addition in different contexts are: Vector addition calculator ; Perimeter of a polygon calculator ; and Velocity addition calculator. Diameter is the largest chord which passes through the centre of the circle. The theorems will be based on these topics:. Download Now. Probability Solved Examples. Introduction to Circles. View Result. Segment addition postulate example Segment bisector How do we use the segment addition postulate practically? What is the segment addition postulate? Note: The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide. All about Circles.

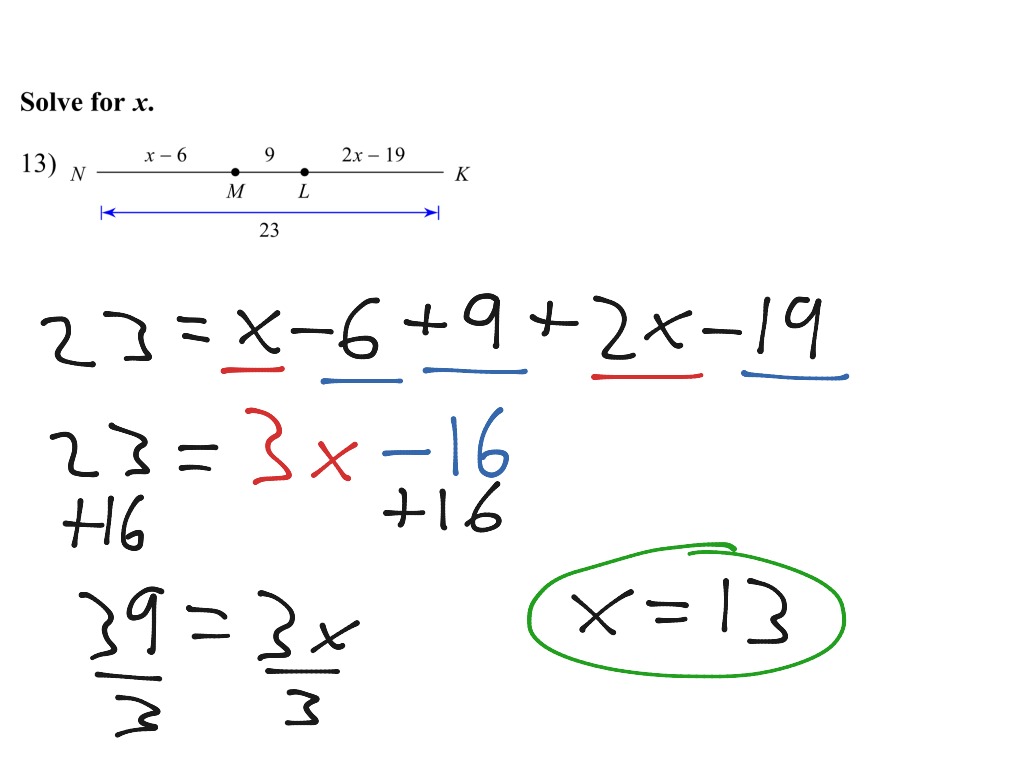
I can look for the reference to a site on which there are many articles on this question.