Sin 90 cos 90

Wzory redukcyjne — wzory pozwalające sprowadzić obliczanie wartości funkcji trygonometrycznych dowolnego kąta skierowanego do obliczenia wartości funkcji dla kąta ostregoa dalej sin 90 cos 90 kąta o mierze z zakresu od 90° do °. W poniższych wzorach używana jest miara łukowa kąta.

Dla Ucznia nauka liceum nauka zdalna portal edukacja technikum Nowa Era sprawdzian fiszki quizy nauka zdalna. Dla Ucznia nauka liceum nauka zdalna portal edukacja technikum Nowa Era. W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Sprawdź się Filmy Materiały dodatkowe. W skrócie Tożsamości trygonometryczne — kąty ostre Tożsamości trygonometryczne to związki między funkcjami trygonometrycznymi. Zyskaj dostęp do setek lekcji przygotowanych przez ekspertów!

Sin 90 cos 90

W tablicach podaje się wartości funkcji trygonometrycznych jedynie dla kątów I ćwiartki. W pozostałych ćwiartkach bowiem występują te same wartości, jedynie ich kolejność może być zmieniona lub znak. Weźmy pod uwagę cztery kąty:. Wzorów redukcyjnych jest dość dużo. Istotne jest nie tyle wyuczenie się ich na pamięć, co umiejętność wyprowadzania tych wzorów. To zaś polega na właściwym odczytywaniu prostych rysunków. Pokazujemy to poniżej na paru przykładach. Wzory dla kąta o -. Rozważmy kąty i o - w położeniu standardowym: Z kątem o - można skojarzyć wyobrażenie obrotu złożonego z obrotu o kąt o i obrotu o kąt -. Oba kąty kreślimy w jednym układzie, zataczamy okrąg i na otrzymanym w ten sposób kole trygonometrycznym odczytujemy rzędne i odcięte punktów M i M' : Rzędne są jednakowe, natomiast odcięte są liczbami przeciwnymi. Stąd odczytujemy, że jest:. Rozważmy kąty i 90 o - w położeniu standardowym rysunek a : Końcowe ramiona tych kątów l i l' są wzajemnie symetryczne względem prostej dwusiecznej kąta XOY. Ponieważ symetria półprostych l i l' zachdzi dla dowolnego , więc dla dowolnego mamy związki. Rozważmy odpowiednie kąty w położeniu standardowym rysunek a : Końcowe ramiona tych kątów są półprostymi l' i l'' położonymi symetrycznie względem osi rzędnych. Stąd wynikają wzory redukcyjne:.

Nie lubisz kupować kota w worku? Weźmy pod uwagę cztery kąty:.

.

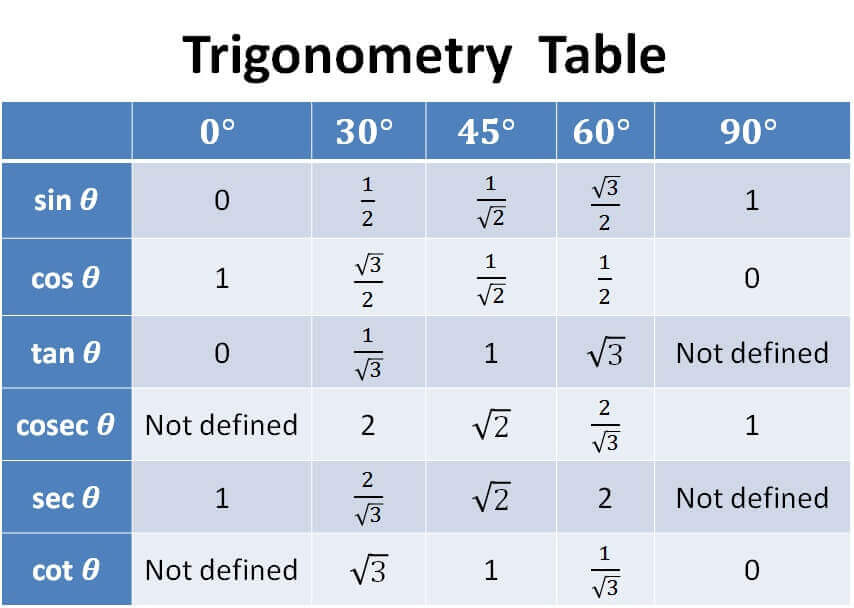
In Trigonometry, different types of problems can be solved using trigonometry formulas. These problems may include trigonometric ratios sin, cos, tan, sec, cosec and cot , Pythagorean identities, product identities, etc. Learning and memorizing these mathematics formulas in trigonometry will help the students of Classes 10, 11, and 12 to score good marks in this concept. They can find the trigonometry table along with inverse trigonometry formulas to solve the problems based on them. Below is the link given to download the pdf format of Trigonometry formulas for free so that students can learn them offline too. Trigonometry is a branch of mathematics that deals with triangles. Trigonometry is also known as the study of relationships between lengths and angles of triangles. There are an enormous number of uses of trigonometry and its formulae. For example, the technique of triangulation is used in Geography to measure the distance between landmarks; in Astronomy, to measure the distance to nearby stars and also in satellite navigation systems. Put your understanding of this concept to test by answering a few MCQs.

Sin 90 cos 90

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Introduction to the trigonometric ratios. About About this video Transcript. Sin, cos, and tan are trigonometric ratios that relate the angles and sides of right triangles. Sin is the ratio of the opposite side to the hypotenuse, cos is the ratio of the adjacent side to the hypotenuse, and tan is the ratio of the opposite side to the adjacent side. They are often written as sin x , cos x , and tan x , where x is an angle in radians or degrees. Created by Sal Khan. Want to join the conversation?

Great lakes holistics muskegon

Stąd wynikają wzory redukcyjne:. Kategoria : Twierdzenia trygonometrii. Składniki cytoplazmy Zobacz lekcję. Miesięczny dostęp do wszystkich przedmiotów. Należy pamiętać, że funkcje trygonometryczne są okresowe — jeżeli miara kąta przekracza ° można wyodrębnić z niej wielokrotność ° i przeprowadzać obliczenia dla pozostałej części. W poniższych wzorach używana jest miara łukowa kąta. Pokazujemy to poniżej na paru przykładach. Wzory dla kąta o -. Dla Ucznia nauka liceum nauka zdalna portal edukacja technikum Nowa Era sprawdzian fiszki quizy nauka zdalna Dla Ucznia nauka liceum nauka zdalna portal edukacja technikum Nowa Era. Zobacz też [ edytuj edytuj kod ] trygonometria funkcje trygonometryczne tożsamości trygonometryczne. Lubisz naukę z dlaucznia. Przełącz ograniczenie szerokości strony. Sprawdź się Filmy Materiały dodatkowe. Wzory redukcyjne można wywieść z symetrii wykresów odpowiednich funkcji trygonometrycznych.

The value of sin 90 degrees is 1. In this article, we will discuss the methods to find the value of sin 90 degrees with examples.

Interpretacja na wykresie [ edytuj edytuj kod ] Wykresy pozwalają też na wyobrażenie sobie i szybkie odtworzenie w pamięci lub na kartce wzorów redukcyjnych. Czytaj Edytuj Edytuj kod źródłowy Wyświetl historię. Lubisz naukę z dlaucznia. Sprawdź się Filmy Materiały dodatkowe. Wzory redukcyjne — wzory pozwalające sprowadzić obliczanie wartości funkcji trygonometrycznych dowolnego kąta skierowanego do obliczenia wartości funkcji dla kąta ostrego , a dalej dla kąta o mierze z zakresu od 90° do ° W poniższych wzorach używana jest miara łukowa kąta. Pokazujemy to poniżej na paru przykładach. W pozostałych ćwiartkach bowiem występują te same wartości, jedynie ich kolejność może być zmieniona lub znak. Wzory redukcyjne można wywieść z symetrii wykresów odpowiednich funkcji trygonometrycznych. W skrócie Tożsamości trygonometryczne — kąty ostre Tożsamości trygonometryczne to związki między funkcjami trygonometrycznymi. Stąd odczytujemy, że jest:. Miesięczny dostęp do wszystkich przedmiotów. Dla Ucznia nauka zdalna liceum nauka zdalna portal W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Składniki cytoplazmy Zobacz lekcję. Kategoria : Twierdzenia trygonometrii.