Sin inverse cos 43 pi by 5
Cyfrowe sygnały mogą być analizowane w dziedzinie czasu oraz w dziedzinie częstotliwości. Algorytmy działające w dziedzinie czasu operują bezpośrednio na próbkach cyfrowego sygnału. Analiza częstotliwościowa sygnału, stosowana w wielu operacjach cyfrowego przetwarzania sygnałów, polega na przekształceniu sygnału z dziedziny czasu do dziedziny częstotliwości. Widmo sygnału ang.
Możliwe jest definiowanie właściwości za pomocą wyrażeń matematycznych. W GUI, pola wyboru lub pola wejściowe, które są powiązane z właściwościami zawierają niebieską ikonę. Wyrażenie FreeCAD jest wyrażeniem matematycznym zgodnym z notacją dla standardowych operatorów matematycznych, funkcji oraz predefiniowanych stałych opisanych poniżej. Dodatkowo, wyrażenie może odwoływać się do innych wyrażeń warunkowych , a także używać warunków. Liczby w wyrażeniu mogą mieć opcjonalnie dołączoną jednostkę. W liczbach można używać przecinka , lub kropki dziesiętnej. Gdy używany jest przecinek, po nim musi następować co najmniej jedna cyfra.
Sin inverse cos 43 pi by 5
.
In [26]:. Sygnał świergotowy jest używany np. Algorytm wykorzystywany przez NumPy jest elastyczny.
.
Solve Practice Play. Game Central. Greatest Common Factor. Least Common Multiple. Order of Operations. Mixed Fractions. Prime Factorization. Solve for a Variable. Evaluate Fractions.
Sin inverse cos 43 pi by 5
This inverse trigonometric functions calculator will help you solve all calculations involving the inverse trigonometric functions. In this article, we'll help you understand what the inverse trigonometric functions are , what the inverse trigonometric functions ranges are , and how to calculate the inverse trigonometric functions. We will also demonstrate some practical examples to help you understand these concepts. Trigonometric functions are mathematical functions that help to describe the relationship between the sides of a right triangle. The most common trigonometric functions are the sine, cosine and tangent, and more rarely you may come across the cotangent, secant and cosecant. You can learn more about this topic with our trigonometric functions calculator and trigonometry calculator. The inverses of these functions are arcsine, arccosine, arctangent, arccotangent, arcsecant and arccosecant. The inverse trigonometric functions ranges and other useful information is summarized in the table below.
Free halloween screensavers for android
W uzyskanym widmie, co druga wartość będzie odpowiadała wartościom widma transformaty o rozmiarze , a pozostałe wartości widma są interpolowane. Aby to zilustrować, obliczymy widmo sygnału świergotowego chirp. Dla częstotliwości Hz, blok próbek zawiera dokładnie okresów sinusa. Pokażemy tutaj najprostszy, klasyczny algorytm Cooleya-Tukeya typu radix-2 , z podziałem czasowym DIT - decimation in time , operujący na ciągach wartości sygnału o długości będącej potęgą liczby 2. Poniższa tabela pokazuje zarówno rozdzielczość częstotliwościową, jak i czasową. Jeśli przekształcenie dotyczy Rotation , zwróconym obiektem jest Placement. Milli kelwin. Mega niuton. Algorytm działa następująco. Okno Blackmana powoduje największe poszerzenie prążka. Po drugie, zwiększa się w ten sposób rozdzielczość czasową analizy. Zgodnie z oczekiwaniami, widzimy trzy prążki na częstotliwościach składowych sinusów. Przy pierwszym zapisie dokumentu wybieramy nazwę pliku, która zazwyczaj różni się od początkowej domyślnej nazwy "Nienazwany1".
.
Popatrzmy co się dzieje dla sygnału sinusoidalnego o częstotliwości Hz, a więc w sytuacji, gdy dla okna o długości próbek nie ma przecieków. Możemy wziąć np. Widzimy, że w oby przypadkach "złapaliśmy" inną chwilową częstotliwość sygnału. In [1]:. Następnie można nadal wprowadzać zmiany w pliku i jego arkuszu kalkulacyjnym, ale nie należy modyfikować jego nazwy. Czy zatem większy rozmiar transformaty jest zawsze lepszy? Dlatego duże rozmiary FFT stosujemy dla sygnałów o stabilnym widmie, gdy zależy nam na dokładnym rozróżnieniu składowych częstotliwościowych. Nazwy obiektów takich jak wymiary, szkice itp. Odchylenie standardowe wartości argumentów. Jeżeli okno prostokątne nie obejmuje wielokrotności okresu sygnału, rzeczywiste widmo sygnału i widmo okna prostokątnego "rozjeżdżają się" przy obliczaniu splotu. Możemy użyć progowania i szukać dla każdego prążka pierwszej i ostatniej wartości powyżej progu.

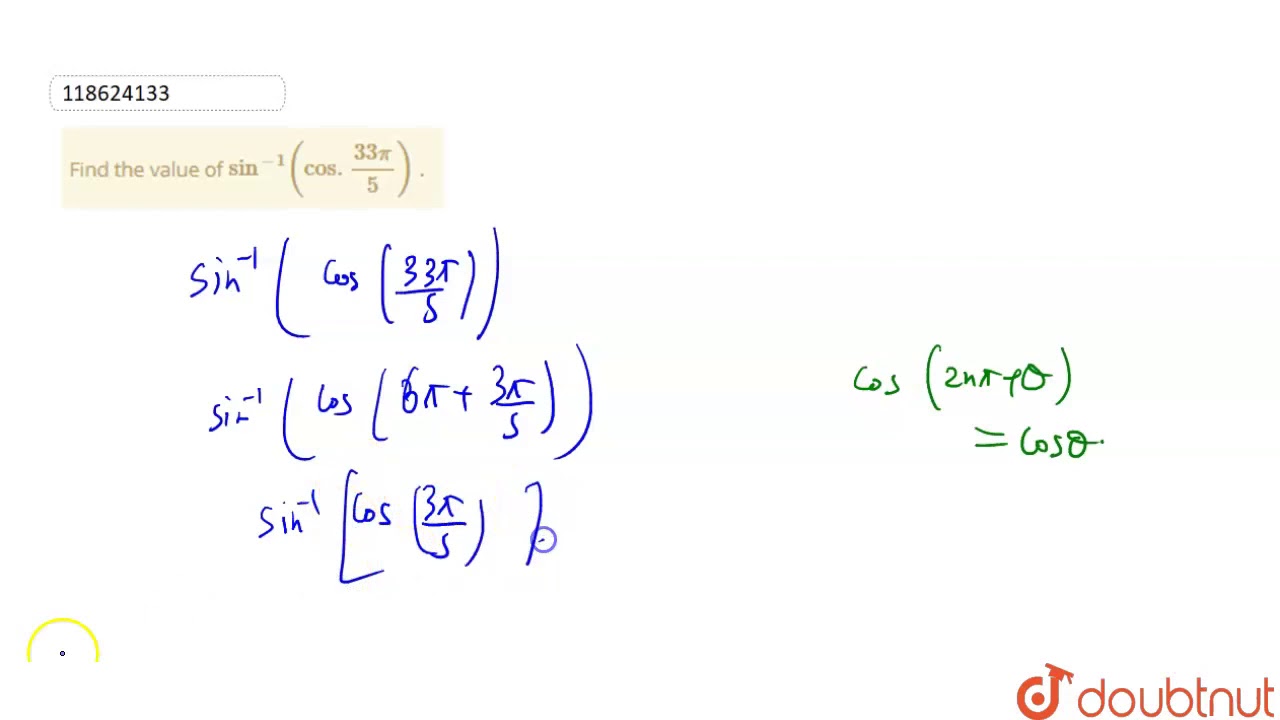
Completely I share your opinion. In it something is also to me it seems it is good idea. I agree with you.