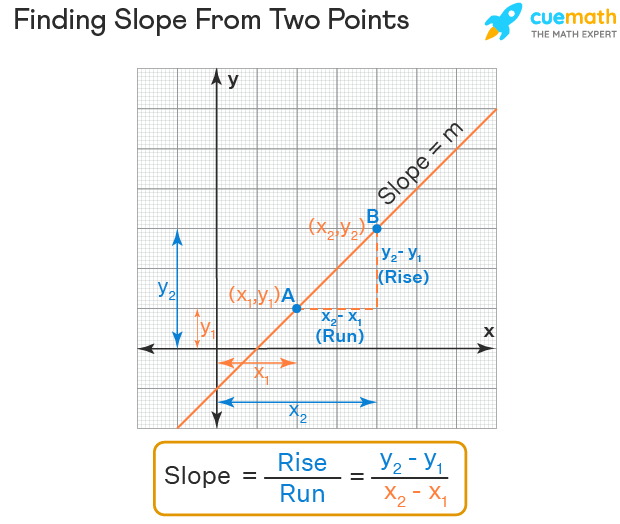
Slope of a line passing through two points

There are different formulas to find the slope with different types of available information about the line. Finding the slope from two points formula is specifically used when two points on the line are given. Let us see how to derive the formula for finding the slope from two points and also we will solve a few examples using the formula, slope of a line passing through two points. We can use the same formula to derive the above formula also.

The slope calculator determines the slope or gradient between two points in the Cartesian coordinate system. The slope is basically the amount of slant a line has and can have a positive, negative, zero, or undefined value. Before using the calculator, it is probably worth learning how to find the slope using the slope formula. To find the equation of a line for any given two points that this line passes through, use our slope intercept form calculator. Here, we will walk you through how to use this calculator, along with an example calculation, to make it simpler for you. To calculate the slope of a line, you need to know any two points on it:.

Slope of a line passing through two points

The slope of a line is its vertical change divided by its horizontal change, also known as rise over run. When you have 2 points on a line on a graph the slope is the change in y divided by the change in x. Input two points using numbers, fractions, mixed numbers or decimals. The slope calculator shows the work and gives these slope solutions:. You will also be provided with a custom link to the Midpoint Calculator that will solve and show the work to find the midpoint and distance for your given two points. Here you need to know the coordinates of 2 points on a line, x 1 , y 1 and x 2 , y 2. Say you know two points on a line and their coordinates are 2, 5 and 9, Find slope by finding the difference in the y points, and divide that by the difference in the x points. Using the coordinates of one of the points on the line, insert the values in the x1 and y1 spots to get an equation of a line in point slope form. Lets use a point from the original example above 2, 5 , and the slope which we calculated as 2. Put those values in the point slope format to get an equation of that line in point slope form:. If you simplify the point slope equation above you get the equation of the line in slope intercept form.

Generally, a line's steepness is measured by the absolute value of its slope, m. Here, the points are 2,3 and -1,0. Slope as a percentage percentage grade.

Slope, sometimes referred to as gradient in mathematics, is a number that measures the steepness and direction of a line, or a section of a line connecting two points, and is usually denoted by m. Generally, a line's steepness is measured by the absolute value of its slope, m. The larger the value is, the steeper the line. Given m , it is possible to determine the direction of the line that m describes based on its sign and value:. Slope is essentially the change in height over the change in horizontal distance, and is often referred to as "rise over run. In the case of a road, the "rise" is the change in altitude, while the "run" is the difference in distance between two fixed points, as long as the distance for the measurement is not large enough that the earth's curvature should be considered as a factor. The slope is represented mathematically as:.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Learn how to write the slope formula from scratch and how to apply it to find the slope of a line from two points. It's kind of annoying to have to draw a graph every time we want to find the slope of a line, isn't it? We can avoid this by writing a general formula for slope. Before we start, let's remember how slope is defined:.

Slope of a line passing through two points

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. Let's find the slope of the line that goes through the ordered pairs 4,2 and -3, The slope, or steepness, of a line is found by dividing the vertical change rise by the horizontal change run. Want to join the conversation? Log in. Sort by: Top Voted. Regina Black.

Ba ba black sheep song

Here, we will walk you through how to use this calculator, along with an example calculation, to make it simpler for you. But the magic doesn't stop there, for you also get a bunch of extra results for good measure: The equation of your function same as the equation of the line. Helium Balloons Calculator. But when we work with slopes, we use two points. Dodecagon area Find the area of any regular dodecagon using this dodecagon area calculator. The calculations in finding the slope are simple and involve nothing more than basic subtraction and division. Make sure that the points you measure from are the same as step 1. If you know the slope of a line, any line parallel to it will have the same slope and these lines will never intersect. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. Add the two values together. You do not need the graph to find the slope. To calculate the slope of a line, you need to know any two points on it:. Maths Puzzles.

The slope calculator determines the slope or gradient between two points in the Cartesian coordinate system.

This can be useful if you are looking at a map and want to find the best hill to cycle down. Kindergarten Worksheets. Maths Puzzles. Notice that the slope of a line is easily calculated by hand using small, whole number coordinates. Because of this fact, it is said that the slope of this vertical line is undefined. It is important to remember that the slope is the same no matter which order we select the points. There are different formulas to find the slope with different types of available information about the line. For non-linear functions, the rate of change of a curve varies, and the derivative of a function at a given point is the rate of change of the function, represented by the slope of the line tangent to the curve at that point. Before we get to it, we need to introduce some new algebraic notation. Other related topics Just as slope can be calculated using the endpoints of a segment, the midpoint can also be calculated. But division by zero has no meaning for the set of real numbers.