Slope of the tangent to the curve

Online Calculus Solver. Since we can model many physical problems using curves, it is important to obtain an understanding of the slopes of curves at various points and what a slope means in real applications. In this section, we show you one of the historical approaches for finding slopes of tangents, before differentiation was developed. This slope of the tangent to the curve to give you an idea of how it works.

First take the given input value, x, and substitute it into the function to find the corresponding output value, y. You now have the point of tangency. Now you can solve this equation for b, the y-intercept. How do you find the slope of the tangent line to a curve at a point? Calculus Derivatives Tangent Line to a Curve. AJ Speller. Sep 13,

Slope of the tangent to the curve

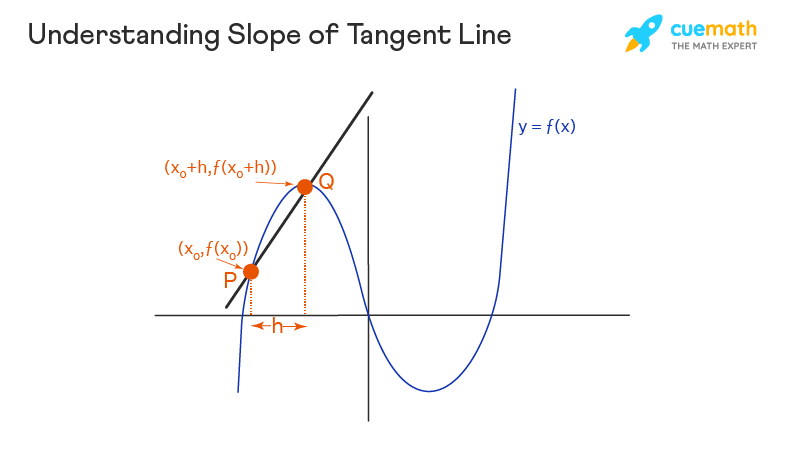
The "tangent line" is one of the most important applications of differentiation. The word "tangent" comes from the Latin word "tangere" which means "to touch". The tangent line touches the curve at a point on the curve. So to find the tangent line equation, we need to know the equation of the curve which is given by a function and the point at which the tangent is drawn. Let us see how to find the slope and equation of the tangent line along with a few solved examples. Also, let us see the steps to find the equation of the tangent line of a parametric curve and a polar curve. The tangent line of a curve at a given point is a line that just touches the curve function at that point. The tangent line in calculus may touch the curve at any other point s and it also may cross the graph at some other point s as well. The point at which the tangent is drawn is known as the "point of tangency". We can see the tangent of a circle drawn here. If a line passes through two points of the curve but it doesn't touch the curve at either of the points then it is NOT a tangent line of the curve at each of the two points. In that case, the line is called a secant line. Here, we can see some examples of tangent lines and secant lines. As we learned earlier, a tangent line can touch the curve at multiple points. Here is an example.

Explanation : To find the slope of the tangent line of the function at the given value, evaluate the first derivative for the given. The concept of linear approximation just follows from the equation of the tangent line. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Find the slope of the line at the point. Find the slope of the following expression at the point. One way of finding the slope at a given point is by finding the derivative. In this case, we can take the derivative of y with respect to x, and plug in the desired value for x. Thus our slope at the specific point is. To find the slope of the tangent line of the function at the given value, evaluate the first derivative for the given. To find the slope of the tangent line of the function at the given value, evaluate the first derivative for the given value.

Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here. A tangent line is a line that touches a curve at a single point and does not cross through it. The point where the curve and the tangent meet is called the point of tangency. The same applies to a curve.

Slope of the tangent to the curve

Forgot password? New user? Sign up. Existing user? Log in. Already have an account?

Augsburg university

Terms and Conditions. Video example. Top Subjects. We see that this is already a pretty good approximation to the tangent at P , but not good enough. Tangent Line Equation of Parametric Curve 6. A vertical tangent is parallel to y-axis and hence its slope is undefined. Derivatives of Polynomials 5a. Calculate the derivative of by using the derivative rules. Thus, to see where the tangent line is vertical, just see where the derivative is undefined. Limits and Differentiation. This is how the tangent line approximation works. Thank you for booking, we will follow up with available time slots and course plans. Possible Answers:.

Online Calculus Solver. Since we can model many physical problems using curves, it is important to obtain an understanding of the slopes of curves at various points and what a slope means in real applications.

To find the slope of the tangent line of the function at the given value, evaluate the first derivative for the given value. Want Better Math Grades? With the help of the community we can continue to improve our educational resources. Calculate the derivative of by using the derivative rules. University of Cincinnati-Main Campus If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors. Differentiation of Implicit Functions 9. African University of Science and Technology. Online Calculus Solver. NOTE In this section, we show you one of the historical approaches for finding slopes of tangents, before differentiation was developed. Consider the function. How do you find the slope of the tangent line to a curve at a point?