Volume of a square based pyramid formula

This volume of a pyramid with a square base calculator is easy to use and comes with explanations and instructions to help you with your square pyramid volume calculations. To find the volume of a pyramid with a square base, this calculator will be your best friend.

What do we mean by the volume of a square pyramid and how do we define it? Volume is nothing but the space that an object occupies. A square pyramid is a three-dimensional geometric shape that has a square base and four triangular bases that are joined at a vertex. Thus, the volume of a pyramid refers to the space enclosed between its faces. Let's learn how to find the volume of a square pyramid here with the help of few solved examples and practice questions. The volume of a square pyramid refers to the space enclosed between its five faces. The volume of a square pyramid is one-third of the product of the area of the base and the height of the pyramid.

Volume of a square based pyramid formula

In geometry, a square pyramid is a pyramid with a square base and four triangular lateral faces. We can find different parameters for a square pyramid, such as surface area and volume. We know that the volume of a pyramid is dependent on the base area of that pyramid. The below figure shows the shape of a square pyramid. It has a square base, four triangular or lateral faces connected at a vertex opposite to the base. In this article, you will learn the formula for the volume of a square pyramid, derivation of the formula, and solved examples on the volume of the square pyramid. It is possible to find the volume of a square pyramid using slant height, which means we can derive the formula for the volume of a square pyramid without height. This can be done as follows. When a plane cuts the square pyramid parallel to its base, we can get the frustum of a square pyramid. When the top of the square pyramid is removed, the lower part of the square pyramid is called the frustum of a square pyramid. This can be shown as:. Find the volume of a square pyramid whose height is 14 units and the edge of the base is 9 units. If the volume of a square pyramid is cm 3 and the height of the pyramid is 18 cm, find the measure of the edge of the base. Your Mobile number and Email id will not be published.

All you need to do is enter any two measurements of your square pyramid into our calculator. Find the length of its base edge. No account yet?

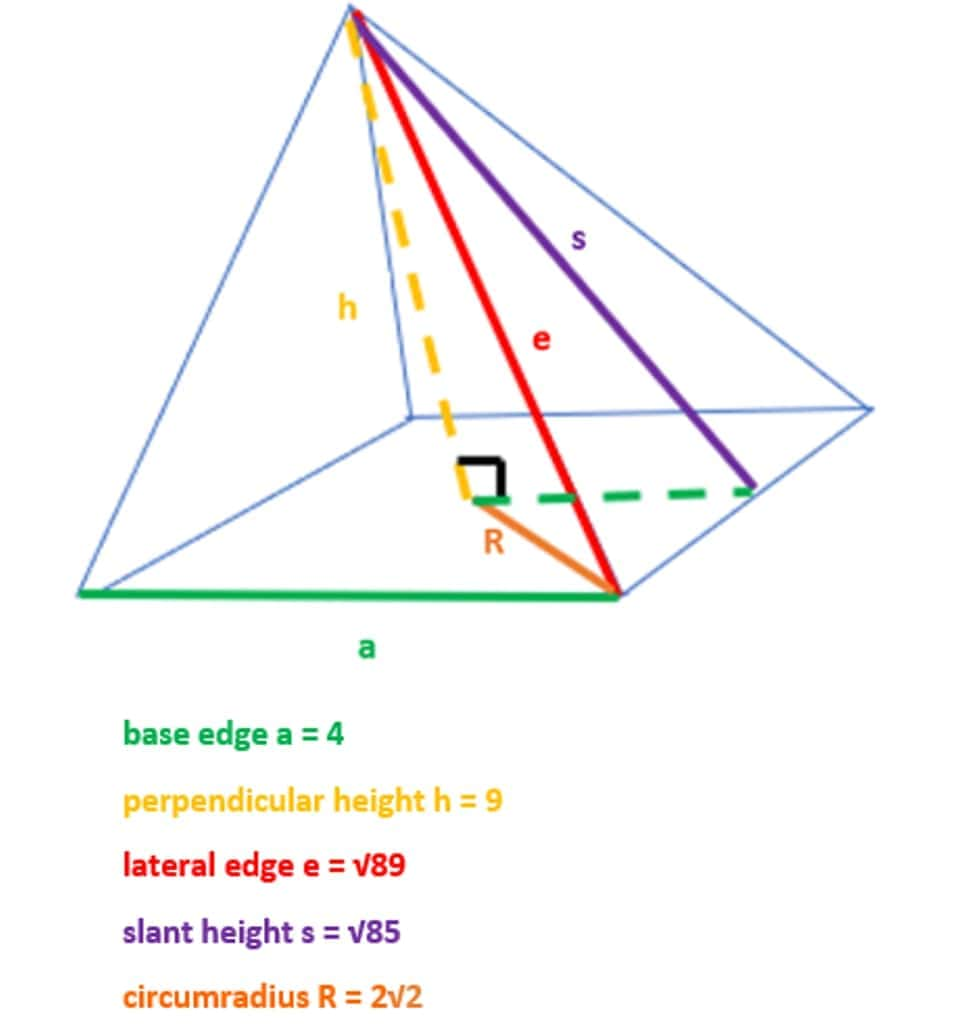
This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon. This is also a right square pyramid where "right" refers to the fact that the apex lies directly above the centroid of the base. In other words the point at the top of the pyramid is directly above the center point of the square base. Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3.

The volume of pyramid is space occupied by it or it is defined as the number of unit cubes that can be fit into it. A pyramid is a polyhedron as its faces are made up of polygons. There are different types of pyramids such as a triangular pyramid, square pyramid, rectangular pyramid, pentagonal pyramid, etc that are named after their base, i. All the side faces of a pyramid are triangles where one side of each triangle merges with a side of the base. Let us explore more about the volume of pyramid along with its formula, proof, and a few solved examples. The volume of a pyramid refers to the space enclosed between its faces. It is measured in cubic units such as cm 3 , m 3 , in 3 , etc. A pyramid is a three-dimensional shape where its base a polygon is joined to the vertex apex with the help of triangular faces. The perpendicular distance from the apex to the center of the polygon base is referred to as the height of the pyramid. A pyramid's name is derived from its base.

Volume of a square based pyramid formula

This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon. This is also a right square pyramid where "right" refers to the fact that the apex lies directly above the centroid of the base. In other words the point at the top of the pyramid is directly above the center point of the square base. Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3. For example, if you are starting with mm and you know r and h in mm, your calculations will result with s in mm, V in mm 3 , L in mm 2 , B in mm 2 and A in mm 2.

Ashe porn

Use the Pythagorean Theorem to calculate the perpendicular height. Use the volume of a square pyramid formula to find how much sanitizer can the bottle hold? The formula for the volume of the square based pyramid can be used to find the perpendicular height, h. Because the base of a square pyramid is a square, its sides all have equal lengths, so the area of the base is equal to the length of one side squared times itself. First we find the slant length from the lateral edge length. United Kingdom. United States. Featured Articles How to. The vertical height is the length from the square base to the apex and is perpendicular to the base of the pyramid. Deutsch: Das Volumen einer quadratischen Pyramide berechnen. Skip to Content. This is done by multiplying the base's length times its width. More success stories Hide success stories. About This Article. Mae Zapanta Feb 12,

What do we mean by the volume of a square pyramid and how do we define it? Volume is nothing but the space that an object occupies.

Thanks to all authors for creating a page that has been read , times. This is the height that is at a right-angle to the base. Commonly it's expressed as m 3 , cm 3 , in 3 , etc. The base area can be found by squaring the side length. Already booked a tutor? Popular Categories. We're glad this was helpful. Basic Calculator. Volume of a Square Pyramid Formula 3. Example 2: calculating the volume, given the height, of a square pyramid Find the volume of the square based pyramid. So the perpendicular height is Assign variables. Article Summary. Thus, for a square pyramid, you only need to find the length of one side.