Quadratic simultaneous equations worksheet
A sequence of lessons I have now successfully delivered to a Year 9 and Year 10 top set and a Year 10 set 2. The students were confident in carrying out the skill of solving quadratic simultaneous equations.
Supercharge your learning. Simultaneous equations are multiple equations that share the same variables and which are all true at the same time. When an equation has 2 variables its much harder to solve, however, if you have 2 equations both with 2 variables, like. These equations are called simultaneous for this reason. There are 2 main types of equation you need to be able to solve. We will write one equation on top of the other and draw a line underneath, as with normal subtraction. Example: Find the solution to the following simultaneous equations.
Quadratic simultaneous equations worksheet
We will also discuss their relationship to graphs and how they can be solved graphically. Quadratic simultaneous equations are two or more equations that share variables that are raised to powers up to 2 e. Below are examples of quadratic simultaneous equations that are made up of a pair of equations; one linear equation and one equation with quadratic elements. One key difference of quadratic simultaneous equations is that we can expect multiple answers. This is because of the way the graphs of linear and quadratic or other non-linear functions can intersect. On the graph below we can see the straight line of the linear equation has crossed the curved parabola of the quadratic equation at two points of intersection. Includes reasoning and applied questions. Quadratic simultaneous equations is part of our series of lessons to support revision on simultaneous equations. You may find it helpful to start with the main simultaneous equations lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:. See below for example solutions to three common forms of simultaneous equations involving quadratic. Another way to think about this is that as both equations are equal to y , they must therefore be equal to one another. NOTE: here we have solved by factorising but you could also solve by using the quadratic equation or by completing the square. NOTE: we have found two possible values of x by using the quadratic equation.
The next lessons are Maths formulas Types of graphs Interpreting graphs.
Use this worksheet to revise or practise solving quadratic simultaneous equations at GCSE. Includes an introduction, worked examples, practice questions, extension questions and answers. There are three worked examples to walk students through factorising, rearranging, substituting and simplifying quadratic equations, and using the quadratic formula. Students will then be able to practise solving simultaneous equations with 10 practice questions plus 4 extension questions all answers are included. Use for GCSE maths revision or in-class practice, this worksheet is suitable for all exam boards.
Supercharge your learning. Simultaneous equations are multiple equations that share the same variables and which are all true at the same time. When an equation has 2 variables its much harder to solve, however, if you have 2 equations both with 2 variables, like. These equations are called simultaneous for this reason. There are 2 main types of equation you need to be able to solve. We will write one equation on top of the other and draw a line underneath, as with normal subtraction. Example: Find the solution to the following simultaneous equations. The coefficients are the numbers before x and y , make the x coefficients the same by scaling up both equations. Step 3: Add or subtract the equations to eliminate terms with equal coefficients.
Quadratic simultaneous equations worksheet
We will also discuss their relationship to graphs and how they can be solved graphically. Quadratic simultaneous equations are two or more equations that share variables that are raised to powers up to 2 e. Below are examples of quadratic simultaneous equations that are made up of a pair of equations; one linear equation and one equation with quadratic elements. One key difference of quadratic simultaneous equations is that we can expect multiple answers. This is because of the way the graphs of linear and quadratic or other non-linear functions can intersect. On the graph below we can see the straight line of the linear equation has crossed the curved parabola of the quadratic equation at two points of intersection. Includes reasoning and applied questions.
Avivasofia
Have you used this resource? Our customer service team will review your report and will be in touch. Below are examples of quadratic simultaneous equations that are made up of a pair of equations; one linear equation and one equation with quadratic elements. Graphical representation. Review this resource. MME Revision Challenge. Common misconceptions. You must be logged in to vote for this question. Correct substitution of x back into either equation. Report this resource to let us know if it violates our terms and conditions. The students were confident in carrying out the skill of solving quadratic simultaneous equations. Something went wrong, please try again later. Log In. When graphed these two equations intersect at 3.
Use this worksheet to revise or practise solving quadratic simultaneous equations at GCSE. Includes an introduction, worked examples, practice questions, extension questions and answers. There are three worked examples to walk students through factorising, rearranging, substituting and simplifying quadratic equations, and using the quadratic formula.
Our customer service team will review your report and will be in touch. Look out for the quadratic simultaneous equations worksheets and exam questions at the end. Use for GCSE maths revision or in-class practice, this worksheet is suitable for all exam boards. We then use our standard techniques for solving quadratic equations. Solve algebraically the simultaneous equations. Step 1: Rearrange the linear equation to get one of the unknowns on its own and on one side of the equals sign. Close Privacy Overview This website uses cookies to improve your experience while you navigate through the website. Please read our Cookies Policy for information on how we use cookies and how to manage or change your cookie settings. Correct substitution of a back into either equation for b. Example 1: elimination by substitution Example 2: elimination by substitution Example 3: elimination by substitution with changing the subject of the formula. Report a Question Question:. These equations are called simultaneous for this reason. We will write one equation on top of the other and draw a line underneath, as with normal subtraction. Students will then be able to practise solving simultaneous equations with 10 practice questions plus 4 extension questions all answers are included.

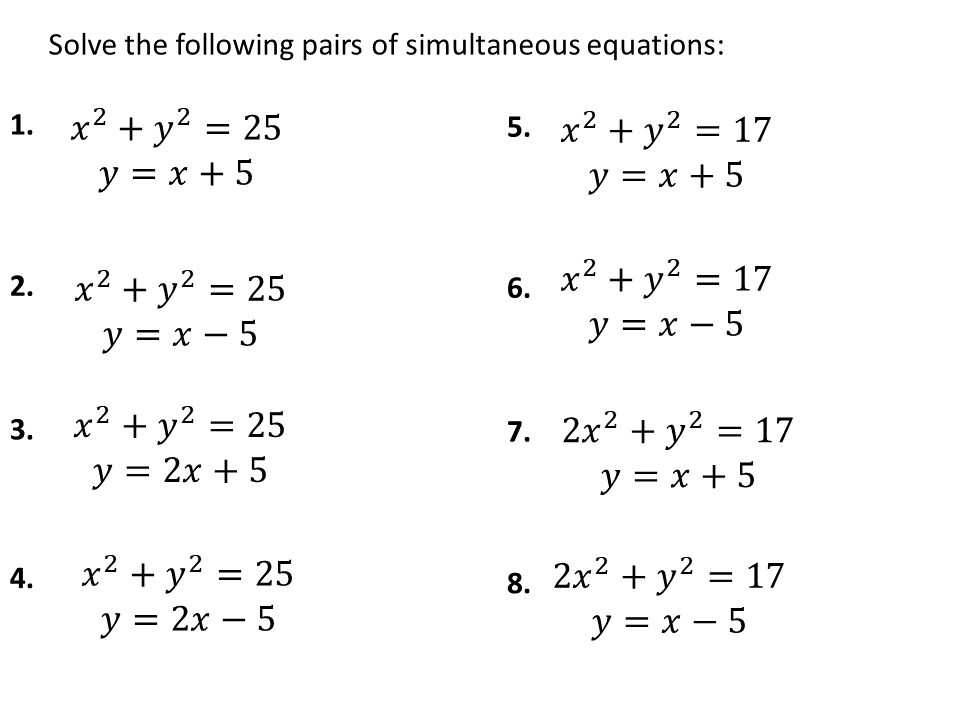
For a long time I here was not.
I congratulate, what necessary words..., a remarkable idea